Bounded Static Analysis

Everything Everywhere All at Once

What is Bounded Static Analysis?
Abstractions
Bounded Abstract Interpretation
Getting Started

Proposal due Wednesday Evening after fall break.

But you can hand it in before.

Questions

Why should we use abstractions when analysing code?
What is the advantage of Galoi connections?
Which cases are the Sign abstraction not able to catch?
At which cases do your static analysis outperform your dynamic?

Feedback

Is this still fun?

What is Bounded Static Analysis? (§1)

In Theory (§1.1)

Breath-first!

{𝚜 𝚝 𝚎 𝚙}_{P} (T) = {τ^{'} s | s \in Σ, τ^{'} \in T, δ_{P} ({τ^{'}}_{| τ^{'} |}, s)}

\begin{matrix} {𝚜 𝚝 𝚎 𝚙}_{P}^{0} & = I_{P} \\ {𝚜 𝚝 𝚎 𝚙}_{P}^{n} & = {𝚜 𝚝 𝚎 𝚙}_{P} ({𝚜 𝚝 𝚎 𝚙}_{P}^{n - 1}) \cup {𝚜 𝚝 𝚎 𝚙}_{P}^{n - 1} \end{matrix}

\begin{matrix} {𝐁 𝐒 𝐀}_{P}^{n} & = {𝚜 𝚝 𝚎 𝚙}_{P}^{n} \end{matrix}

{𝐁 𝐀 𝐄}_{P}^{n} \equiv \exists (τ s) \in {𝐁 𝐒 𝐀}_{P}^{n} \land s = err (‘𝚊𝚜𝚜𝚎𝚛𝚝𝚒𝚘𝚗 𝚎𝚛𝚛𝚘𝚛’)

May and Must Analyses (§1.2)

\begin{matrix} {𝚜 𝚝 𝚎 𝚙}_{𝗆 𝗎 𝗌 𝗍} (T) \subseteq 𝚜 𝚝 𝚎 𝚙 (T) \subseteq {𝚜 𝚝 𝚎 𝚙}_{𝗆 𝖺 𝗒} (T) \end{matrix}

{𝚜 𝚝 𝚎 𝚙}_{𝗆 𝗎 𝗌 𝗍}^{n} \subseteq {𝚜 𝚝 𝚎 𝚙}^{n} \subseteq {𝚜 𝚝 𝚎 𝚙}_{𝗆 𝖺 𝗒}^{n}

\begin{matrix} {𝐁 𝐀 𝐄}_{𝗆 𝗎 𝗌 𝗍}^{n} ⟹ {𝐁 𝐀 𝐄}^{n} \\ \neg {𝐁 𝐀 𝐄}^{n} ⟸ \neg {𝐁 𝐀 𝐄}_{𝗆 𝖺 𝗒}^{n} \end{matrix}

Abstractions (§2)

The Sign Analysis
Partially Ordered Sets (Posets)
Lattices
Galois Connection
Abstract Operations

The Sign Analysis (§2.1)

𝐒 𝐢 𝐠 𝐧 = {+, 0, -}

$α$ is the abstractor

\begin{matrix} α ({1, 2, 3}) = & {+} \\ α ({0}) = & {0} \\ α ({- 1, 3}) = & {+, -} \\ α ({- 1, 0, 3}) = & {0, +, -} \end{matrix}

Fasten your seatbelts it's going to be a bumby night!

Partially Ordered Sets (Posets) (§2.2)

A partially ordered set $(L, ⊑)$

\begin{matrix} reflexive & \forall a . a ⊑ a \\ antisymetric & \forall a . a ⊑ b \land b ⊑ a ⟹ a = b \\ transitive & \forall a . a ⊑ b \land b ⊑ c ⟹ a ⊑ c \end{matrix}

Examples

Integers in both directions $(ℤ, \geq)$ $(ℤ, \leq)$
Sets $({𝚝 𝚝, 𝚏 𝚏}, \Rightarrow)$
Signed $(2^{𝐒 𝐢 𝐠 𝐧}, \subseteq)$

Why Partial Orders?

Lattices (§2.3)

Partial orders $(L, ⊑_{L})$ ,
meet $⊓$ ,
join $⊔$ ,
and has a smallest and biggest element.

Hasse diagrams. (§2.3.1)

A Hasse diagram over the poset $(2^{𝐒 𝐢 𝐠 𝐧}, \subseteq)$ . By I, KSmrq, CC BY-SA 3.0 (with edits)

Back to the Sign Abstraction (§2.3.2)

$⊑_{𝐒 𝐢 𝐠 𝐧} = \subseteq$ , $⊥ = \emptyset$ , and $⊤ = {+, -, 0}$

Galois Connection (§2.4)

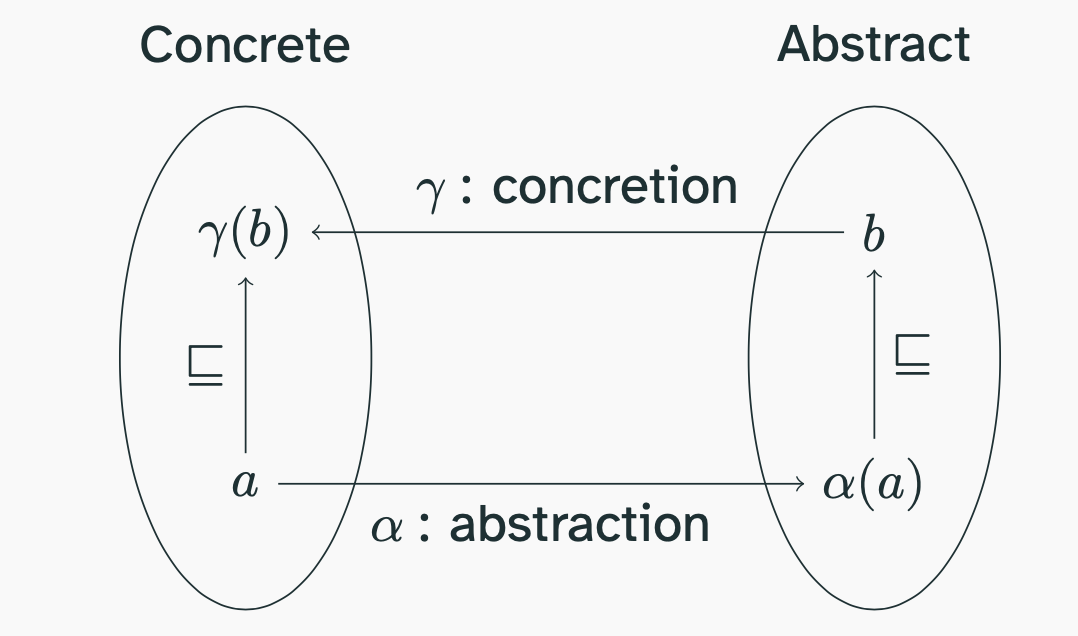
\forall a \in C, b \in A . a ⊑_{C} γ (b) \Leftrightarrow α (a) ⊑_{A} b

(A Galois Connection is a connection between two ordered sets, with a concretion $γ$ and an abstraction $α$ function.)

What are they good for?

A mathematical definition of one-sided information loss. If my abstraction finds a bug, is there a bug in the original domain?
A weak equality.

Laws For Free

\begin{matrix} c ⊑_{C} γ (α (c)) & – if we abstract we only increase in size \\ α (γ (a)) ⊑_{A} a & – if we concertize we only decrease in size \\ α (γ (α (c))) = α (c) & – we don’t keep loosing information \\ γ (α (γ (a))) = γ (a) & – in both directions \\ γ (a_{1} ⊔_{A} a_{2}) = γ (a_{1}) ⊔_{C} γ (a_{2}) & – γ preserves joins. \\ α (c_{1} ⊓_{C} c_{2}) = α (c_{1}) ⊓_{A} α (c_{2}) & – α preserves meets. \end{matrix}

Adjunctions and Testing

# Most of the time
parse(pretty(a)) == a 

# Always
pretty(parse(pretty(a))) == pretty(a)

# Bonus for all strings s:
parse(pretty(parse(s))) == parse(s)

Back to the Sign Analysis (§2.4.1)

\begin{matrix} α (N) & = {+ | n \in N, n < 0} \\ \cup {- | n \in N, n > 0} \\ \cup {0 | n \in N, n = 0} \\ γ (S) & = {n | n \in ℤ, n < 0, + \in S} \\ \cup {n | n \in ℤ, n > 0, - \in S} \\ \cup {0 | 0 \in S} \end{matrix}

Build the Sign Abstraction

@classmethod
def abstract(cls, items : set[int]): 
  signset = set()
  if 0 in items:
    signset.add("0")
  ...
  return cls(signset)

def __contains__(self, member : int): 
  if (member == 0 and "0" in self.signs): 
      return True
  ...

Test your abstaction

\forall X \subset 2^{ℤ} : X \subseteq γ (α (X))

from hypothesis import given
from hypothesis.strategies import integers, sets

@given(sets(integers()))
def test_valid_abstraction(xs):
  s = SignSet.abstract(xs) 
  assert all(x in s for x in xs)

Abstract Operations (§2.5)

$A +_{2^{32}} B \subseteq γ (α (A) +_{𝐒 𝐢 𝐠 𝐧} α (B))$

$α (A +_{2^{32}} B) \subseteq α (A) +_{𝐒 𝐢 𝐠 𝐧} α (B)$

Define the operation

\begin{matrix} {+} +_{𝐒 𝐢 𝐠 𝐧} {+} = & {+} & {+} +_{𝐒 𝐢 𝐠 𝐧} {-} = {-, +, 0} \\ {+} +_{𝐒 𝐢 𝐠 𝐧} {0} = & {+} & {0} +_{𝐒 𝐢 𝐠 𝐧} {+} = {+} \\ {0} +_{𝐒 𝐢 𝐠 𝐧} {-} = & {-} & {0} +_{𝐒 𝐢 𝐠 𝐧} {0} = {0} \\ {-} +_{𝐒 𝐢 𝐠 𝐧} {+} = & {-, +, 0} & {-} +_{𝐒 𝐢 𝐠 𝐧} {-} = {-} \\ {-} +_{𝐒 𝐢 𝐠 𝐧} {0} = & {-} & \dots \end{matrix}

Test your Abstract Operation

@given(sets(integers()), sets(integers()))
def test_sign_adds(xs, ys):
  assert (
    SignSet.abstract({x + y for x in xs for y in ys}) 
      <= SignSet.abstract(xs) + SignSet.abstract(ys)
    )

Bounded Abstract Interpretation (§3)

$(2^{𝐓 𝐫 𝐚 𝐜 𝐞}, \subseteq) \leftrightarrow_{γ}^{α} (A, ⊑_{A})$ ${𝐁 𝐒 𝐀}_{A}^{n} = {𝚜 𝚝 𝚎 𝚙}_{A}^{n}$

\begin{matrix} {𝚜 𝚝 𝚎 𝚙}_{A}^{0} & = α (I_{P}) \\ {𝚜 𝚝 𝚎 𝚙}_{A}^{n} & = {𝚜 𝚝 𝚎 𝚙}_{A} ({𝚜 𝚝 𝚎 𝚙}_{A}^{n - 1}) ⊔_{A} {𝚜 𝚝 𝚎 𝚙}_{A}^{n - 1} \end{matrix}

To show ${𝐁 𝐒 𝐀}^{n} \subseteq γ ({𝐁 𝐒 𝐀}_{A}^{n})$ , we need to prove:

𝚜 𝚝 𝚎 𝚙 (T) \cup T \subseteq γ ({𝚜 𝚝 𝚎 𝚙}_{A} (α (T)) ⊔_{A} α (T)) .

But we can get away with

α (𝚜 𝚝 𝚎 𝚙 (T)) ⊑_{A} {𝚜 𝚝 𝚎 𝚙}_{A} (α (T))

The State Abstraction (§3.1)

(2^{𝐓 𝐫 𝐚 𝐜 𝐞}, \subseteq) \leftrightarrow_{γ}^{α} (2^{𝐒 𝐭 𝐚 𝐭 𝐞}, \subseteq)

\begin{matrix} α (T) = {τ_{| τ |} | τ \in T} \\ γ (S) = {τ | s \in S, τ \in 𝐓 𝐫 𝐚 𝐜 𝐞, τ_{| τ |} = s} \end{matrix}

{𝚜 𝚝 𝚎 𝚙}_{𝐒 𝐭 𝐚 𝐭 𝐞} (S) = {s^{'} | s \in S, δ (s, s^{'})}

This is nice because

if $err (‘𝚊𝚜𝚜𝚎𝚛𝚝𝚒𝚘𝚗 𝚎𝚛𝚛𝚘𝚛’) \notin {𝐁 𝐒 𝐀}_{𝐒 𝐭 𝐚 𝐭 𝐞}^{n}$ , then
$\neg \exists τ . τ err (‘𝚊𝚜𝚜𝚎𝚛𝚝𝚒𝚘𝚗 𝚎𝚛𝚛𝚘𝚛’) \in {𝐁 𝐒 𝐀}^{n}$

The Per-Instruction Abstraction (§3.2)

𝐏 𝐜 = ι \to 2^{𝐒 𝐭 𝐚 𝐭 𝐞}

(2^{𝐒 𝐭 𝐚 𝐭 𝐞}, \subseteq) \leftrightarrow_{γ}^{α} (𝐏 𝐜, ⊑_{𝐏 𝐜})

{𝚜 𝚝 𝚎 𝚙}_{𝐏 𝐜} (C) = ⨆_{𝐏 𝐜} {ι^{'} \mapsto {⟨ σ^{'}, λ^{'}, ι^{'} ⟩} | \begin{matrix} (ι \mapsto S) \in C, S^{'} = {𝚜 𝚝 𝚎 𝚙}_{ι} (S), \\ ⟨ σ^{'}, λ^{'}, ι^{'} ⟩ \in S^{'} \end{matrix}}

The Per-Variable Abstraction (§3.3)

𝐏 𝐯 = ι \to (ℕ \mapsto (2^{𝐕_{σ}})) \times (2^{𝐕_{σ}}) * \cup {ok, err (‘.’)}

(𝐏 𝐜, ⊑_{𝐏 𝐜}) \leftrightarrow_{γ}^{α} (𝐏 𝐯, ⊑_{𝐏 𝐯})

Variable Abstractions (§3.4)

𝐏 𝐯 [A] = ι \to (ℕ \mapsto A) \times A * \cup {ok, err (‘.’)}

(2^{𝐕_{σ}}, \subseteq) \leftrightarrow_{γ}^{α} (A, ⊑_{A}) ⟹ (𝐏 𝐯, ⊑_{𝐏 𝐯}) \leftrightarrow_{γ}^{α} (𝐏 𝐯 [A], ⊑_{𝐏 𝐯 [A]})

(𝐏 𝐯, ⊑_{𝐏 𝐯}) \leftrightarrow_{γ}^{α} (𝐏 𝐯 [𝐒 𝐢 𝐠 𝐧], ⊑_{𝐏 𝐯 [𝐒 𝐢 𝐠 𝐧]})

Abstractions All The Way Down. (§3.5)

\begin{matrix} (2^{𝐓 𝐫 𝐚 𝐜 𝐞}, \subseteq) & \leftrightarrow_{γ}^{α} (2^{𝐒 𝐭 𝐚 𝐭 𝐞}, \subseteq) \\ \leftrightarrow_{γ}^{α} (𝐏 𝐜, ⊑_{𝐏 𝐜}) \\ \leftrightarrow_{γ}^{α} (𝐏 𝐯, ⊑_{𝐏 𝐯}) \\ \leftrightarrow_{γ}^{α} (𝐏 𝐯 [𝐒 𝐢 𝐠 𝐧], ⊑_{𝐏 𝐯 [𝐒 𝐢 𝐠 𝐧]}) \end{matrix}

Getting Started (§4)

Abstract Your Interpreter
Emit multiple states.
Start Small, Just One frame.

Emit multiple States

def step(state : AState) -> Iterable[AState | str]
  ...

Do all states at once.

def many_step(state : dict[Pc, AState | str]) 
  -> dict[Pc, AState | str]:
  new_state = dict(state)
  for k, v in state.items():
      for s in step(v):
        new_state[s.pc] |= s
  return new_state

Questions

Why should we use abstractions when analysing code?
What is the advantage of Galoi connections?
Which cases are the Sign abstraction not able to catch?
At which cases do your static analysis outperform your dynamic?

Bounded Static Analysis

Table of Contents

Questions

What is Bounded Static Analysis? (§1)

In Theory (§1.1)

May and Must Analyses (§1.2)

Abstractions (§2)

The Sign Analysis (§2.1)

Partially Ordered Sets (Posets) (§2.2)

Examples

Why Partial Orders?

Lattices (§2.3)

Hasse diagrams. (§2.3.1)

Back to the Sign Abstraction (§2.3.2)

Galois Connection (§2.4)

What are they good for?

Laws For Free

Adjunctions and Testing

Back to the Sign Analysis (§2.4.1)

Build the Sign Abstraction

Test your abstaction

Abstract Operations (§2.5)

Define the operation

Test your Abstract Operation

Bounded Abstract Interpretation (§3)

To show 𝐁𝐒𝐀n⊆γ(𝐁𝐒𝐀An), we need to prove:

But we can get away with

The State Abstraction (§3.1)

This is nice because

The Per-Instruction Abstraction (§3.2)

The Per-Variable Abstraction (§3.3)

Variable Abstractions (§3.4)

Abstractions All The Way Down. (§3.5)

Getting Started (§4)

Emit multiple States

Do all states at once.

Questions

To show ${𝐁 𝐒 𝐀}^{n} \subseteq γ ({𝐁 𝐒 𝐀}_{A}^{n})$ , we need to prove: