Module 6: Functions and the RISC-V Calling Convention
Contents
Module 6: Functions and the RISC-V Calling Convention#
In this module we study how to add functions to the Hygge0 programming language. On the specification side, functions are not very complicated. However, their code generation is very dependent on the specifics of the target hardware architecture — and for this reason, we will need to study the RISC-V calling convention.
Overall Objective#
Our goal is to interpret, compile and run Hygge programs like the one shown in Example 35 below.
Example 35 (A Hygge Program with Functions)
1// A simple function: takes two integer arguments and returns an integer.
2fun f(x: int, y: int): int = x + y;
3
4// A function instance (a.k.a. lambda term), with a function type annotation:
5// g is a function that takes two integer arguments and returns an integer.
6let g: (int, int) -> int = fun (x: int, y: int) -> x + y + 1;
7
8let x = f(1, 2); // Applying ("calling") a function
9let y = g(1, 2); // Applying ("calling") a lambda abstraction
10assert(x + 1 = y);
11
12// A function that defines a nested function and calls it.
13fun h(x: int): int = {
14 fun privateFun(z: int): int = z + 2;
15 privateFun(x)
16};
17
18let z = h(40);
19assert(z = 42);
20
21// A function that takes a function as argument, and calls it.
22fun applyFunToInt(f: (int) -> int,
23 x: int): int =
24 f(x);
25
26assert(applyFunToInt(h, 1) = 3);
27
28// A function that defines a nested function and returns it.
29fun makeFun(addOne: bool): (int) -> int =
30 if (addOne) then {
31 fun inc(x: int): int = x + 1;
32 inc
33 } else {
34 fun (x: int) -> x + 2
35 };
36
37let plusOne = makeFun(true); // Type: (int) -> int
38let plusTwo = makeFun(false); // Type: (int) -> int
39assert(plusOne(42) = 43);
40assert(plusTwo(42) = 44);
41assert((makeFun(true))(42) = 43)
To introduce functions in the Hygge specification, and make it possible to write programs like the one in Example 35, we follow typical conventions of functional programming languages:
we treat functions as first-class values that can be passed and returned. Such values are also called lambda terms or lambda abstractions (where “lambda” is the greek letter \(\lambda\)).
to “call” a function, we apply a function (or an expression that reduces into a function) to other values; result of the application is a new value;
we introduce a new function type to specify what type of arguments a function expects, and what type of value it returns.
Important
The extensions described in this Module are already partially implemented in the
upstream Git repositories of hyggec at the tag
functions: you should pull and merge the relevant changes into your project
compiler. The Project Ideas of this Module further
extend Hygge with better support for functions.
Syntax#
Definition 21 below extends the syntax of Hygge with functions and function applications, and with a new pretype that specifies the syntax of a new function type. It also introduces a short-hand notation for defining functions.
Definition 21 (Functions and Applications)
We define the syntax of Hygge0 with functions by extending Definition 1 with a new expressions, a new value, and a new pretype:
We also define the following syntactic sugar that provides a shorter way to define a named function:
which is shorthand for the following Hygge expression:
The expansion of syntactic sugar into actual Hygge grammar elements is called desugaring.
In Definition 21 above, a function instance (a.k.a. lambda term) is written “\(\hygLambda{x_1: t_1, \ldots, x_n: t_n}{e}\)”, and it consists of:
zero or more formal arguments \(x_1, \ldots, x_n\), each one annotated with a pretype; and
the function body \(e\), which is executed when the function is applied to actual arguments in order to produce a value (see below).
A function instance (a.k.a. lambda term) can be “called” through an application “\(\hygApp{e}{e_1, \ldots, e_n}\)”, which means that the expression \(e\) (which is expected to reduce into a function instance) is applied to zero or more expressions \(e_1,\ldots,e_n\): each of these expressions should reduce into a value, that becomes an actual argument of the function application. (For more details, see the Operational Semantics below.)
A function pretype “\(\tFun{t_1, \ldots, t_n}{t}\)” is the syntactic description of the type of a function that takes zero or more arguments having type \(t_1, \ldots, t_n\), and returns a value of type \(t\). Just like the other pretypes in Hygge0, we will need to resolve this new pretype into a valid function type: we will address this later, when discussing the Typing Rules.
Finally, the syntactic sugar in Definition 21 provides a convenient syntax for a very typical case: the definition of a named function with a certain \(\textit{name}\) and arguments. This syntax is desugared into a (more verbose) “let…” binder that defines a variable called \(\textit{name}\), having a function type, and initialised with a lambda term. This way, Hygge programmers can have a convenient syntax, without extending the Hygge grammar with a new dedicated expression. (Notice that, had we extended the grammar with a new dedicated expression, we would have also needed to specify how to handle the new expression in the semantics, type checking rules, etc.)
Example 36 (Syntactic Sugar for Function Definitions)
Using the syntactic sugar in Definition 21, we can write:
The expression above is just an alias for the following desugared expression:
In other words, the syntactic sugar above defines regular “let” binding that:
introduces a variable with the given name (in this case, \(f\)) and a function type, and
initialises the variable with a function instance (a.k.a. lambda term) of the corresponding type.
In the scope of this “let”, it is possible to call the function instance by simply applying the newly-defined variable \(f\) to some arguments, e.g. as \(f(2, 3)\).
Operational Semantics#
Definition 22 formalises how substitution works for function instances and applications.
Definition 22 (Substitution for Functions and Applications)
We extend Definition 2 (substitution) with the following new cases:
According to Definition 22:
if a substitution is applied to a function instance “\(\hygLambda{x_1: t_1, \ldots, x_n: t_n}{e}\)”, then the substitution is propagated through the body of the function \(e\) — unless the variable being substituted coincides with one of the function arguments \(x_i\) (for some \(i \in 1..n\)). This is because the function instance acts as a binder for its arguments, hence if an argument is called \(x\), then any reference to \(x\) in the function body \(e\) is referring to that argument \(x\) (i.e. any other variable \(x\) defined in the surrounding scope is shadowed);
if a substitution is applied to an application \(\hygApp{e}{e_1, \ldots, e_n}\), then the substitution is propagated throughout \(e\) (the expression being applied) and the application arguments (\(e_1,\ldots,e_n\)).
We can now introduce the semantics of function application, in Definition 23 below.
Definition 23 (Semantics of Functions and Applications)
We define the semantics of Hygge0 with functions and applications by extending Definition 4 with the following rules:
Given an application “\(\hygApp{e}{e_1, \ldots, e_n}\)”, the reduction rules in Definition 23 work as follows:
rule \(\ruleFmt{R-App-Eval-L}\) requires us to first reduce \(e\), i.e. the expression being applied;
when the expression being applied reduces into a value, rule \(\ruleFmt{R-App-Eval-Ri}\) allows us to reduce the application arguments \(e_1, \ldots, e_n\), proceeding from left to right, until all of them become values;
finally, rule \(\ruleFmt{R-App-Res}\) allows us to perform the actual application. This rule requires that:
the value being applied is a function instance (i.e. a lambda term) \(\hygLambda{x_1: t_1, \ldots, x_n: t_n}{e}\); and
the number of values used as arguments for the application is \(n\), i.e. the same number of arguments expected by the function instance.
When these conditions are met, the application proceeds by taking the body of the function instance \(e\), and replacing each formal argument \(x_i\) with the corresponding actual argument value \(v_i\).
(To see function application in action, see Example 37 below.)
Example 37 (Reduction of Function Application)
Consider again the Hygge program in Example 36 (in its desugared version). Take a runtime environment \(R\) where \(\envField{R}{Printer}\) is defined. The program reduces as follows.
The first reduction uses rule \(\ruleFmt{R-Let-Subst}\) (from Definition 4) to substitute each occurrence of variable \(f\) in the scope of the “let…” with the lambda term that initialises \(f\) (recall that by Definition 21, lambda terms are values and cannot be further reduced).
The second reduction uses rule \(\ruleFmt{R-App-Res}\) (from Definition 23) to apply lambda term to the arguments \((2, 3)\): after the reduction, we obtain the body of the function with argument \(x\) replaced by \(2\), and argument \(y\) replaced by \(3\).
Then, the program continues reducing as expected, by performing the \(\hygPrintln{...}\) and reaching the final value \(5\).
Exercise 29 (Reduction of Function Application)
Write the reductions of the following Hygge expression: (note that you will need to desugar it first)
Typing Rules#
We now discuss how to type-check lambda terms and applications. First, we need to introduce a new function type, formalised in Definition 24 below.
Definition 24 (Function Type)
We extend the Hygge0 typing system with a function type by adding the following case to Definition 5:
In a function type \(\tFun{T_1, \ldots, T_n}{T}\), the types \(T_1,\ldots,T_n\) are the argument types, while \(T\) is the return type.
Example 38
The following function type denotes a function that takes two arguments (an integer and a boolean) and returns a string.
The following function type, instead, denotes a function that:
takes three arguments:
a float,
an integer, and
a function that takes two booleans and returns an integer;
returns a function that takes zero arguments, and returns a unit value.
We also need a way to resolve a syntactic function pretype (from Definition 21) into a valid function type (from Definition 24): this is formalised in Definition 25 below.
Definition 25 (Resolution of Function Types)
We extend Definition 7 (type resolution judgement) with this new rule:
Rule \(\ruleFmt{TRes-Fun}\) in Definition 25 says that, in order to resolve a function pretype “\(\tFun{t_1, \ldots t_n}{t}\)” into a valid function type, we need to:
resolve each argument pretype \(t_i\) (for \(i \in 1..n\)) into a valid type \(T_i\), and
resolve the return pretype \(t\) into a valid type \(T\).
We now have all the ingredients to define the typing rules for lambda terms and applications.
Definition 26 (Typing Rules for Function Instances and Applications)
We define the typing rules of Hygge0 with functions and applications by extending Definition 11 with the following rules (which use the function type introduced in Definition 24 above):
The rules in Definition 26 work as follows.
Rule \(\ruleFmt{T-Fun}\) type-checks a lambda term “\(\hygLambda{x_1: t_1, \ldots, x_n: t_n}{e}\)” in a typing environment \(\Gamma\). In its premises, the rule ensures that all argument variables \(x_1,\ldots,x_n\) are distinct from each other, and each argument pretype \(t_i\) (for \(i \in 1..n\)) is resolved into a valid type \(T_i\). Then, the rule recursively checks whether the function body \(e\) has type \(T\), in a typing environment that extends \(\Gamma\) with the argument variables \(x_1, \ldots x_n\) and their corresponding types: this allows the function body \(e\) to make use of the function argument variables. If all these premises hold, then the rule concludes that the lambda term has the function type \(\tFun{T_1, \ldots, T_n}{T}\).
Rule \(\ruleFmt{T-Fun}\) type-checks an application “\(\hygApp{e}{e_1, \ldots, e_n}\)”. The first premise of the rule checks whether \(e\) (the expression being applied) has a function type \(\tFun{T_1, \ldots, T_n}{T}\). Notice that:
the number of argument types of the function type must be \(n\), which is also the number of arguments in the application; and
the return type \(T\) must be the same type used in the conclusion of the rule.
The second premise of the rule checks whether each application argument \(e_i\) has type \(T_i\) (for \(i \in 1..n\)). If all these premises hold, it means that the application involves an actual function which is given the correct number of arguments, all having the expected types; therefore, the rule concludes that the application has type \(T\) (i.e. the return type of the function being applied).
Example 39 (Type-Checking a Program with Functions and Applications)
Consider this Hygge expression, that defines a function \(f\) and applies it:
To type-check this expression, we first need to desugar it (according to Definition 21), thus obtaining:
For brevity, let us define the following typing environments:
Then, we have the following typing derivation for the desugared expression:
(Download this derivation as a PNG image.)
Let us explore the derivation above, going bottom-up. We begin with the instance of rule \(\ruleFmt{T-Let-T2}\) (from Definition 16).
The first premise of \(\ruleFmt{T-Let-T2}\) resolves the function pretype into an actual function type \(\tFun{\tInt,\tInt}{\tInt}\), using \(\ruleFmt{T-Res-Fun}\) from Definition 25.
The second premise of \(\ruleFmt{T-Let-T2}\) checks whether the expression that initialises \(f\) has the expected type \(\tFun{\tInt,\tInt}{\tInt}\). Since that expression is a lambda term, we type-check it using rule \(\ruleFmt{T-Fun}\) from Definition 26, which:
resolves each pretype assigned to the lambda term arguments \(x\) and \(y\);
type-checks the body of the lambda term (i.e. the expression \(x+y\)) in a typing environment \(\Gamma'\), where \(x\) and \(y\) are mapped to their type \(\tInt\);
concludes that the lambda term has type \(\tFun{\tInt,\tInt}{\tInt}\);
The third premise of \(\ruleFmt{T-Let-T2}\) type-checks the expression in the scope of the “let…”, i.e. \(\hygApp{f}{2,3}\). To this end, it uses a typing environment \(\Gamma''\) where the declared variable \(f\) maps to its type \(\tFun{\tInt,\tInt}{\tInt}\); moreover, since \(\hygApp{f}{2,3}\) is an application, we type-check it using rule \(\ruleFmt{T-App}\) from Definition 26, which:
checks whether the expression being applied (i.e. \(f\)) has a function type;
checks whether \(f\) is applied to exactly two arguments (as expected by its function type), and whether each argument (the expressions \(2\) and \(3\)) has the expected type (\(\tInt\)); and
concludes that the application \(\hygApp{f}{2,3}\) has type \(\tInt\) (i.e. the return type of \(f\)).
Since all premises of this instance of \(\ruleFmt{T-Let-T2}\) hold, the rule concludes that the whole expression has type \(\tInt\).
The RISC-V Memory Layout, Stack, and Calling Convention#
To extend hyggec with support for functions and applications (according to the
specification above) we follow the usual steps, that we discuss later (in the
Implementation section).
However, the code generation step is far from trivial: in order to generate the correct code for functions and applications, we need to be aware of The RISC-V Memory Layout, and the details of Implementing Functions in RISC-V — in particular, the RISC-V calling convention. We now discuss all these topics.
The RISC-V Memory Layout#
When discussing the RISC-V Assembly Program Structure we mentioned that, when a program runs on a RISC-V architecture, its memory is divided into segments — and we highlighted the data segment and the text segment. Fig. 5 shows a more detailed view.
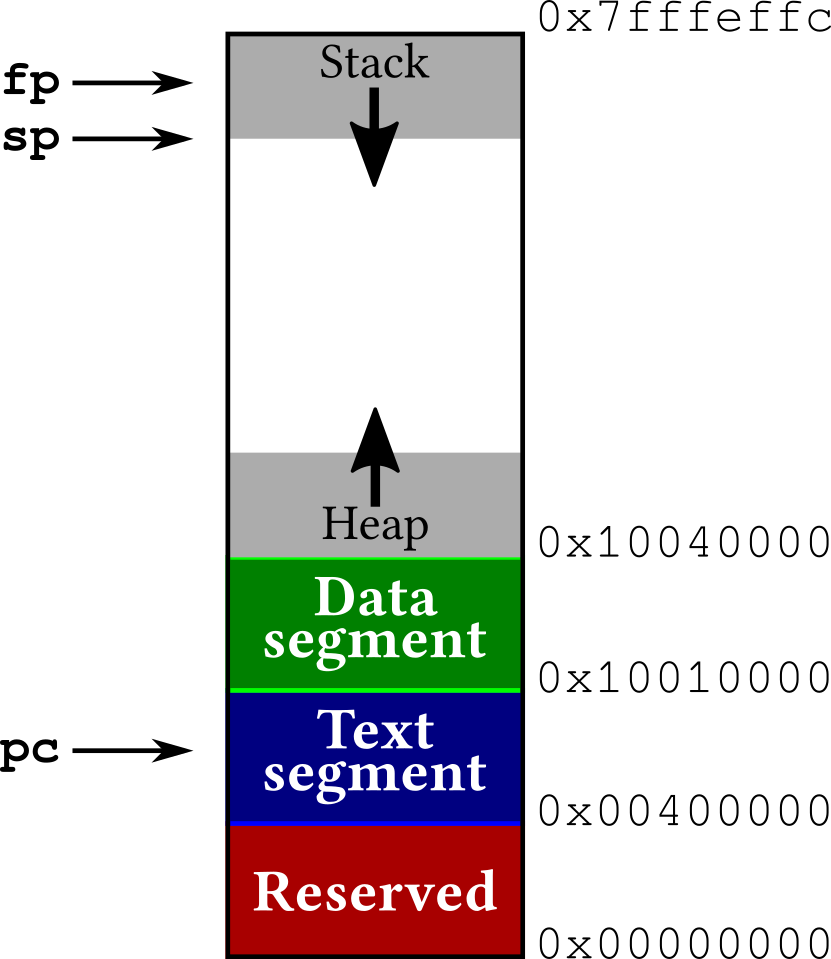
Fig. 5 Typical memory layout of a program running on a RISC-V system. Memory addresses are only indicative.#
Fig. 5 outlines the following memory layout:
the reserved memory area (placed on low memory addresses) is typically used by the operating system;
the text segment contains the program code; the program counter (pc) register should always point to a memory address within this segment;
the data segment contains statically-allocated program data (e.g. constant strings and values);
the heap is a memory area for data allocated dynamically, while the program is running. The heap grows upwards: new data is allocated in higher memory addresses; (we will talk about the heap in the next module)
the stack is also a memory area for dynamically-allocated data — but unlike the heap, it grows downwards (from high to low memory addresses) and its data is allocated and removed in LIFO (last-in-first-out) order. Its main use is to store the local state of a running function: when a function is called, it will add its working data onto the stack, and then remove it before returning to the caller. When a program uses the stack, it leverages two registers:
the stack pointer (sp) register points to the last-allocated memory address on the stack;
the frame pointer (fp) points to the beginning of the current stack frame, i.e. the portion of the stack used by the function that is currently running.
Being a register-based architecture, RISC-V favours using registers instead of memory. However, using the stack becomes hardly avoidable as soon as a program needs to call a function, or perform a system call: we now see why.
Implementing Functions in RISC-V#
We illustrate how functions can be implemented in a RISC-V architecture by first discussing a series of scenarios of growing complexity:
After discussing these scenarios, we conclude with The RISC-V Calling Convention and Its Code Generation (which includes a Detailed Example: the RISC-V Calling Convention in Action).
Calling a Function: a Simple Case#
Consider the following Hygge program, where the “main” program body calls a
function f that immediately returns the same value.
fun f(x: int): int = x;
f(42)
We could compile this program by following a simple convention on how to call a function and return a value, as follows:
the caller of function
f(i.e. the main body of the program) must:write the function call integer arguments in the registers
a0toa7(in this case, we only need to use registera0for the argument42);write the return address in the register
ra(which in fact stands for “return address”). More precisely, the return address is the memory address of the assembly instruction that follows the function callf(1, 2);jump to the memory address where the code of the function
fbegins; andwhen
freturns (i.e. jumps back to the memory address in registerra), find its return value in registera0;
the function
f(i.e. the callee) must:find its integer arguments in registers
a0toa7(in this case, it only uses registera0);compute its result and write it in the return value register
a0; andjump to the memory address in register
ra, thus returning to the caller.
Calling a Function While Saving Temporary Registers#
Consider the following Hygge program, where the “main” body has some local
variables and computation, and calls a function f which also performs some
computation.
fun f(x: int, y: int): int = {
// ... other expressions ...
x + y
};
let a: int = 1 + 1;
let b: int = a + 2;
// ... other expressions ...
f(a, b)
a + b
If we compile this program according to the simple calling convention outlined
in above, we run into a problem. Observe
that (according to the Code Generation Strategy of hyggec):
in the “main” body of the program:
the values of variables
aandbwill be written in the temporary registerst0andt1;the “other expressions” may use further registers — including registers
s0,s1, etc.;
in the body of
f:the result of its “other expressions”, and the result of
x + y, will be written (at least temporarily, before returning) in registert0, and possibly in other registers.
As a consequence, the execution of function f will overwrite the value of
register t0 (and possibly other registers) used by its caller;
consequently, the result of the final expression a + b will be incorrect!
To avoid this scenario, we need to refine the simple calling convention outlined above: we need to save and restore registers to preserve their value. More concretely, the RISC-V conventions specify that some registers should be saved by the caller of a function, while others should be saved by the function being called:
the caller of function
fmust:save on the stack all used registers which are marked as “caller-saved” in the table of RISC-V Base and Floating-Point Registers;
write the integer function arguments in the registers
a0toa7(in this case, we only need to use registersa0anda1for arguments2and42);write the return address (i.e. the memory address of the instruction that follows the call
f(1, 2)) in the registerra(return address);jump to the memory address where the code of the function
fbegins; andwhen
freturns (i.e. jumps back to the memory address in registerra)restore from the stack all caller-saved registers that were saved before calling
f;find the return value of
fin registera0;
the function
f(i.e. the callee) must:save on the stack all the registers it uses which are marked as “callee-saved” in the table of RISC-V Base and Floating-Point Registers;
find its integer arguments in registers
a0toa7(in this case, it only usesa0anda1);compute its result, and write its return value in the register
a0;restore from the stack all callee-saved registers that were saved earlier; and
jump to the return memory address in register
ra.
A Function That Performs a System Call#
Consider the following Hygge program:
fun f(x: int, y: int): int = {
let z = readInt();
x + y + z
};
f(1, 2)
Notice that, in order to perform the system call readInt, the function f
needs to do the following (according to the specification of
RARS System Calls):
write the system call number in register
a7, andfind the system call result in register
a0.
However, by doing so, the system call will overwrite the register a0, that
holds the function argument x!
For this reason, when performing a system call, f needs to proceed as follows:
before the system call, save on the stack any used register between
a0anda7that is also needed by the system call;after the system call, restore from the stack any register between
a0anda7saved earlier.
This can be seen as a special case of
Calling a Function While Saving Temporary Registers: registers a0 to a7 are
“caller-saved”, so they must be saved before calling a function (or before
performing a system call).
Calling a Function with More Than 8 Arguments#
Consider the following Hygge program:
fun g(x1: int, x2: int, ..., x9: int, x10: int): int = {
x1 + x2 + ... + x9 + x10;
};
g(1, 2, ..., 8, 9, 10)
If a function g takes more than 8 arguments, then registers a0 to a7 are
not sufficient for storing all arguments needed to call g. Therefore, we need
to further refine the calling convention outlined
above:
the caller of function
gmust:save on the stack all used registers which are marked as “caller-saved” in the table of RISC-V Base and Floating-Point Registers;
write the first 8 integer function arguments into the registers
a0toa7;write on the stack all integer function arguments above the 8th;
write the return address (i.e. the memory address after the call
g(1, 2, ...)into the registerra(return address);jump to the memory address where the function
gbegins; andwhen
greturns (i.e. jumps back to the memory address in registerra)restore from the stack all caller-saved registers that were saved before calling
f;find the return value of
fin registera0;
the function
g(i.e. the callee) must:save on the stack all the registers it uses which are marked as “callee-saved” in the table of RISC-V Base and Floating-Point Registers;
find its first 8 integer arguments in registers
a0toa7;find the integer arguments above the 8th on the stack;
compute its result, and write its return value into the register
a0;restore from the stack all callee-saved registers that were saved earlier; and
jump to the return memory address in register
ra.
The RISC-V Calling Convention and Its Code Generation#
We can now specify in more detail the RISC-V calling convention, by illustrating how it impacts code generation. To this end, we explore:
the Code Generation for a Function Call; and
a Detailed Example: the RISC-V Calling Convention in Action.
Important
When discussing the RISC-V calling convention below, we say “integer argument”
to actually mean “any function argument whose value (as represented in the
compiled assembly code) can be stored in a base RISC-V integer register”. In
the case of hyggec, such “integer arguments” includes all types of values
except float: so, an “integer argument” (for code generation) includes values
of type int, bool (represented as integer value 0 or 1), and also string
(because strings are represented by their memory address). Values of type unit
have no fixed representation (in fact, hyggec typically discards values of
type unit), but they can harmlessly stored in integer registers.
Code Generation for a Function Instance#
Consider a Hygge function instance (a.k.a. lambda term) \(\hygLambda{x_1:T_1, \ldots, x_n:T_n}{e}\). When generating the assembly code for this function instance, we need to follow these steps.
Generate an assembly label to mark the memory address of the function assembly code (so it can be called later).
Generate the assembly code of a function prologue that:
saves on the stack all registers which are marked as callee-saved in the table of RISC-V Base and Floating-Point Registers, and
initialises the frame pointer register
fpwith the value of the stack pointerspbefore the callee-saved registers were saved.
Generate the assembly the code of the function body \(e\), making sure that it accesses the arguments \(x_1, \ldots, x_n\) by using:
registers
a0…a7for the first 8 integer arguments;registers
fa0…fa7for the first 8 floating-point arguments;the stack for the remaining arguments (if any):
the first argument passed on the stack is located at the memory address contained in the frame pointer register
fp;the following arguments are stored at correspondingly higher addresses.
Generate the assembly the code of a function epilogue that:
copies the value produced by the function body \(e\) into the register
a0(for integer values) orfa0(for float values);restores from the stack all registers that were saved in the prologue;
returns to the caller, by jumping to the memory address in register
ra.
Finally, produce the result of the whole function instance, which is the memory address marked with a label at point 1 above.
Remark 1 (Why Are We Updating the Frame Pointer Register?)
In the explanation above, the use of the frame pointer register fp may seem
redundant: it is just a copy of the value of the stack pointer sp at the
beginning of the function. So, why not just use sp, and keep the fp
register (a.k.a. s0) available for other uses?
Indeed, this is actually possible: using a register as a frame pointer is not
necessary, and RISC-V allows us to use register fp (a.k.a. s0) for any
other purpose. Correspondingly, compilers like gcc and clang include
options (such as -fomit-frame-pointer and -fno-omit-frame-pointer) to
disable or enable the use of a register as frame pointer in the generated code.
As mentioned in The RISC-V Memory Layout, when the register fp is used as frame
pointer, it contains the memory address of the beginning of the portion of the
stack used by a function: this portion of the stack is called function
frame. Storing the starting address of the function frame (i.e., the frame
pointer) in the register fp serves two main purposes.
Using a frame pointer register is convenient for us, compiler writers. This is because:
the value of the frame pointer register
fpnever changes while a function is being executed. Therefore, the code of the function body \(e\) (generated in point 4 above) can usefpto access e.g. arguments passed on the stack with fixed offsets: the first argument will be always at memory address0(fp)(i.e. address infpplus offset 0), the second argument at4(fp)(i.e.fpplus offset 4), etc.;instead, the value of the stack pointer
spchanges every time the code of the function body \(e\) adds more data to the stack. For instance:the first function argument passed on the stack is initially at position
0(sp);however, if the code of \(e\) allocates 1024 bytes on the stack, the value of
spdecreases by 1024: from that point, the compiler must remember that the location of the first argument on the stack is1024(sp).
Keeping track of the changes of
spis possible, but it is tedious and makes the generated assembly harder to understand.
The frame pointer register can be used to inspect the stack of a running program, e.g. by debuggers. By reading the current value of
fp, and knowing the calling convention in use, a debugger can find and identify the local data of a function:the arguments passed on the stack are located in memory addresses equal to or higher than
fp:other data is located in memory addresses lower than
fp.
Code Generation for a Function Call#
Now, consider a function application \(\hygApp{e}{e_1, \ldots, e_n}\). When generating code for this function application, we need to follow these steps.
Generate the assembly code of \(e\) (i.e. the expression being applied as a function): this code should return a memory address produced by a function instance (as described above). We will jump to that address to “call” the function.
Generate the assembly code of each function argument \(e_1, \ldots, e_n\).
Generate “before-call” assembly code that:
saves on the stack all registers which are marked as caller-saved in the table of RISC-V Base and Floating-Point Registers; (when doing this, we can omit saving the target register of the application: its value is not used and it will be overwritten by the return value of the call)
makes sure that the values produced by argument expressions \(e_1, \ldots, e_n\) are in the right place:
the first 8 integer arguments go into registers
a0…a7;the first 8 floating-point arguments go into registers
fa0…fa7;the remaining arguments are written on the stack, in reverse order (i.e. the first argument passed on the stack is written last, in the lowest memory address, and is pointed by the
spregister).
Generate the assembly code that performs the function call, with a jump and link register instruction (
jalr) which does two things:writes the return address in register
ra(such return address is automatically computed by thejalrinstruction itself, as the current value of the program counter registerpc+ 4); andjumps to the memory address returned by expression \(e\) (see point 1 above).
Generate after-call assembly code which, immediately after the function call returns:
moves the result of the function call from register
a0(orfa0) into the target register for the whole function application; andrestores from the stack all registers that were saved in the “before-call” assembly code.
Detailed Example: the RISC-V Calling Convention in Action#
Example 40 below shows how a program with a function call is executed according to the RISC-V calling convention.
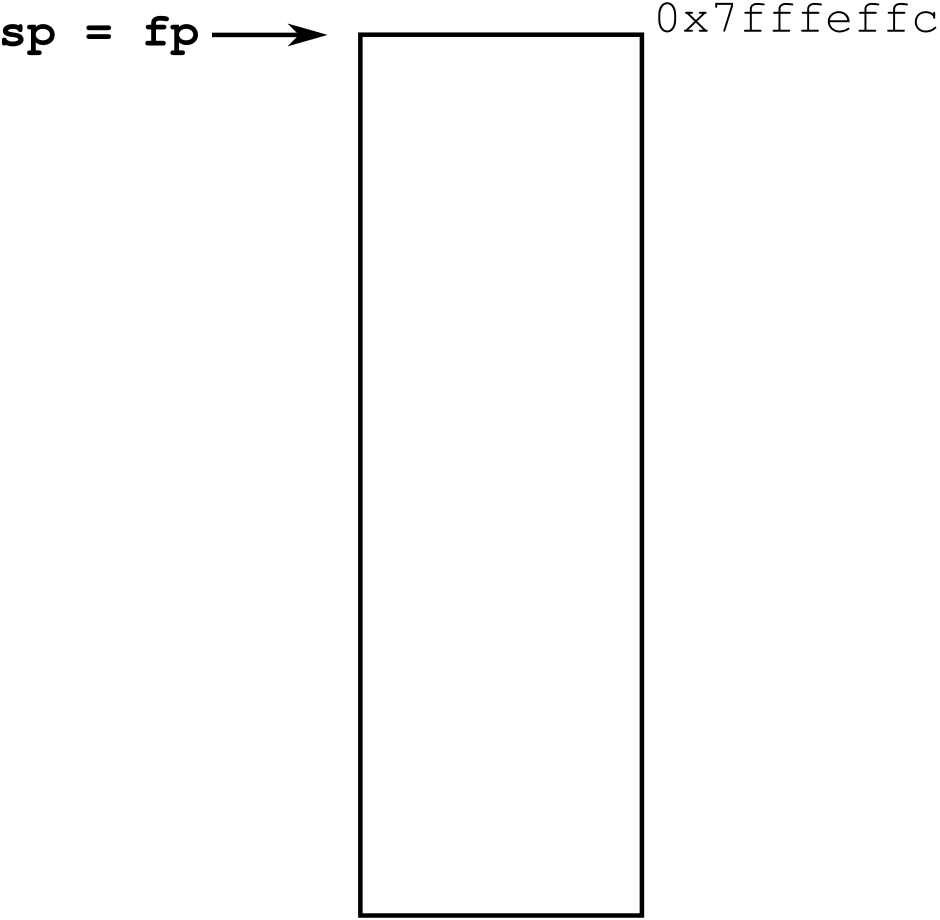
Example 40 (The RISC-V Calling Convention in Action)
Let us explore how a simple Hygge program is expected to manipulate the stack
and registers, according to The RISC-V Calling Convention and Its Code Generation. Each
execution step below is analysed by showing the current state of the program,
registers, and stack, and then discussing them. In the program, the comment
“//<” highlights the current execution point.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
//<
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x00400000
sp = 0x7fffeffc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = ?
t1 = ?
t2 = ?
...
t6 = ?
s1 = ?
...
s4 = ?
s5 = ?
...
|
|
The code, registers, and stack above show that, at the beginning of the
execution, the program counter pc points to the first instruction of the
program, and the stack pointer sp points at the beginning of the stack. The
frame pointer fp is initialised with the same value of sp. The other
registers may be uninitialised, hence they may contain arbitrary values (which
we ignore).
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42; //<
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x00400004
sp = 0x7fffeffc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = 42
t1 = ?
t2 = ?
...
t6 = ?
s1 = ?
...
s4 = ?
s5 = ?
...
|

|
After the first execution step, the program loads value 42 in register t0, and
the program counter pc advences to the next instruction.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x)//<
print(x + y)
|
pc = 0x00400030
sp = 0x7fffeffc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
Then, the program loads the memory address of function f in register t1, and
the values of the function call arguments in registers t2…t6 and
s1…s5.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x)//<
print(x + y)
|
pc = 0x00400080
sp = 0x7fffefbc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|
|
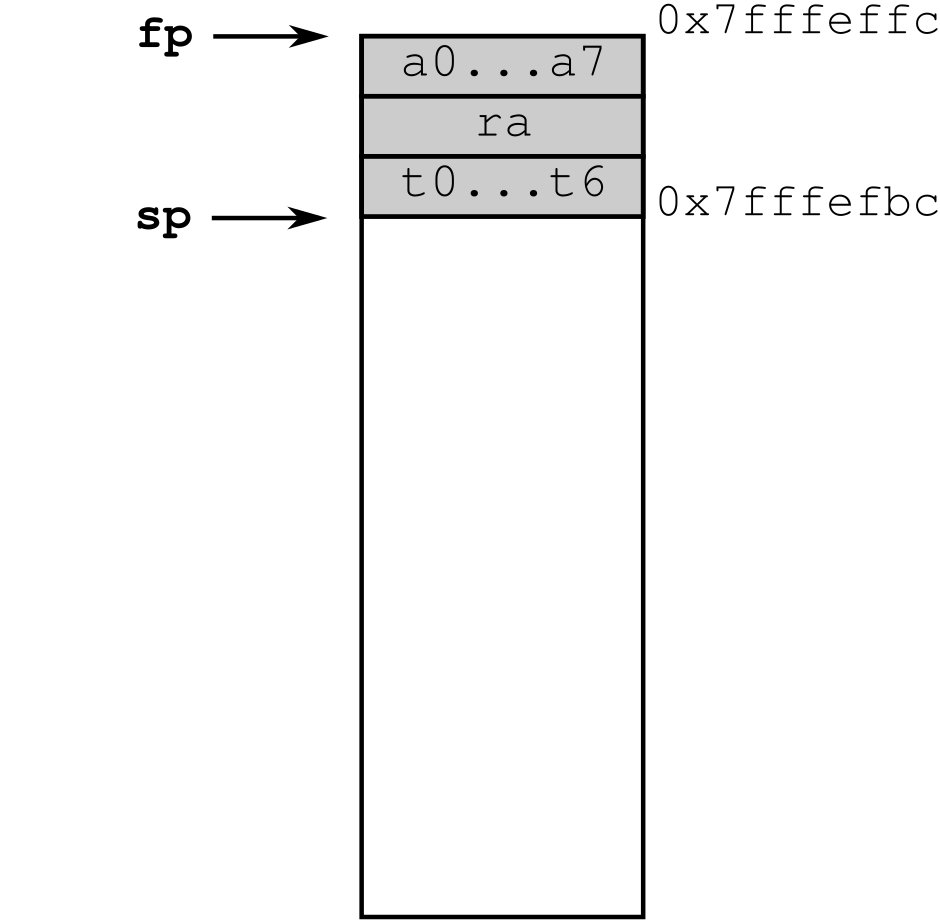
Now, the program starts preparing the function call: it executes the before-call code that saves on the stack all registers that are “caller-saved” (according to the table of RISC-V Base and Floating-Point Registers). Such caller-saved registers consist of:
the argument registers
a0…a7,the return address register
ra, andthe temporary registers
t0…t6.
(For simplicity, here we are only considering integer registers, and we are ignoring the fact that some of them are not currently in use, so saving them is not necessary.)
Observe that the stack pointer sp decreases by 64 bytes (remember that the
stack grows downwards) to make room for saving such 16 registers (of 32 bits
each); the frame pointer fp is not changed.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x)//<
print(x + y)
|
pc = 0x004000a0
sp = 0x7fffefbc
fp = 0x7fffeffc
ra = ?
a0 = 1
...
a7 = 8
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
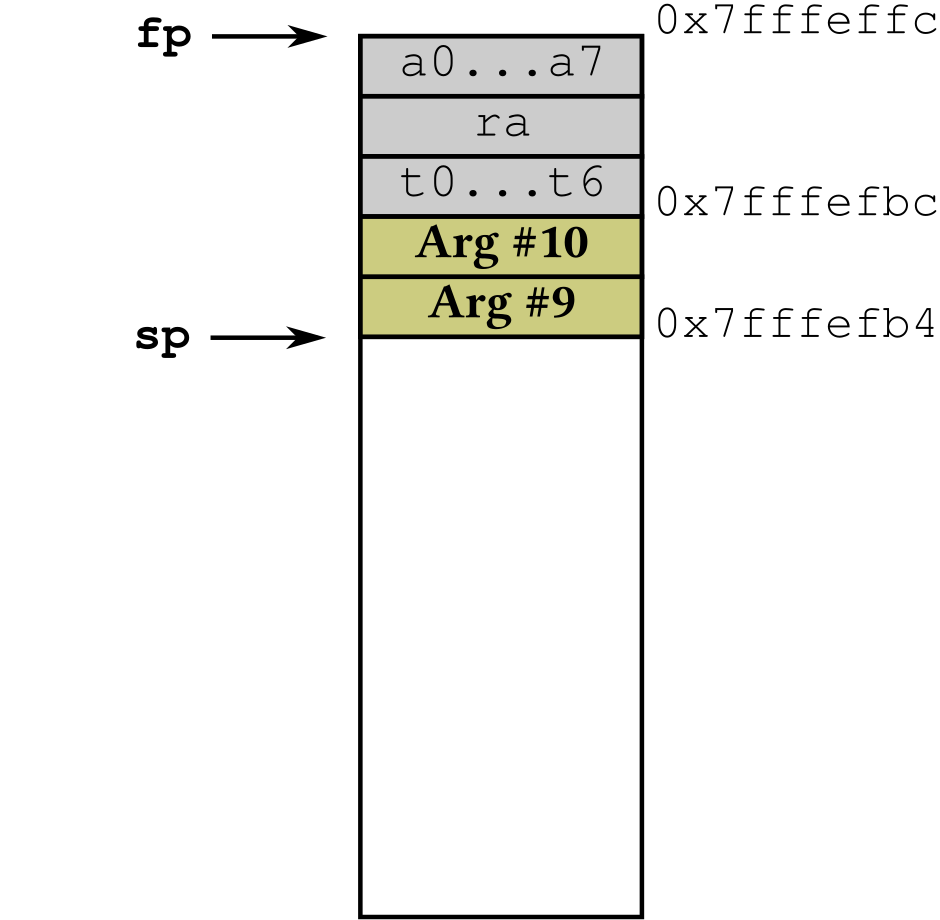
The program keeps preparing the function call: it copies the first 8
arguments of the call into registers a0…a7.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x)//<
print(x + y)
|
pc = 0x004000ac
sp = 0x7fffefb4
fp = 0x7fffeffc
ra = ?
a0 = 1
...
a7 = 8
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|
|
Next, the program copies the function call arguments above the 8th on the stack,
in reverse order (i.e. first argument passed on the stack becomes last, getting
a lower memory address). To this purpose, the program advances the stack
pointer sp by 8 bytes (to make room for 2 arguments, taking 4 bytes each).
(Notice that the frame pointer fp does not change.)
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int, //<
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x00401000
sp = 0x7fffefb4
fp = 0x7fffeffc
ra = 0x004000b0
a0 = 1
...
a7 = 8
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
Now the program performs the function call, invoking the RISC-V assembly
instruction jalr ra, 0(t1), which means:
save in register
rathe return address (which is the value ofpc+ 4), andjump to the memory address computed by taking the value of register
t1and adding the offset0.
After jalr ra, 0(t1) is executed, we have that:
pcis updated with the memory address int1(plus offset0), andthe old value of
pc+ 4 is written in registerra.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int, //<
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x00401038
sp = 0x7fffef84
fp = 0x7fffeffc
ra = 0x004000b0
a0 = 1
...
a7 = 8
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|
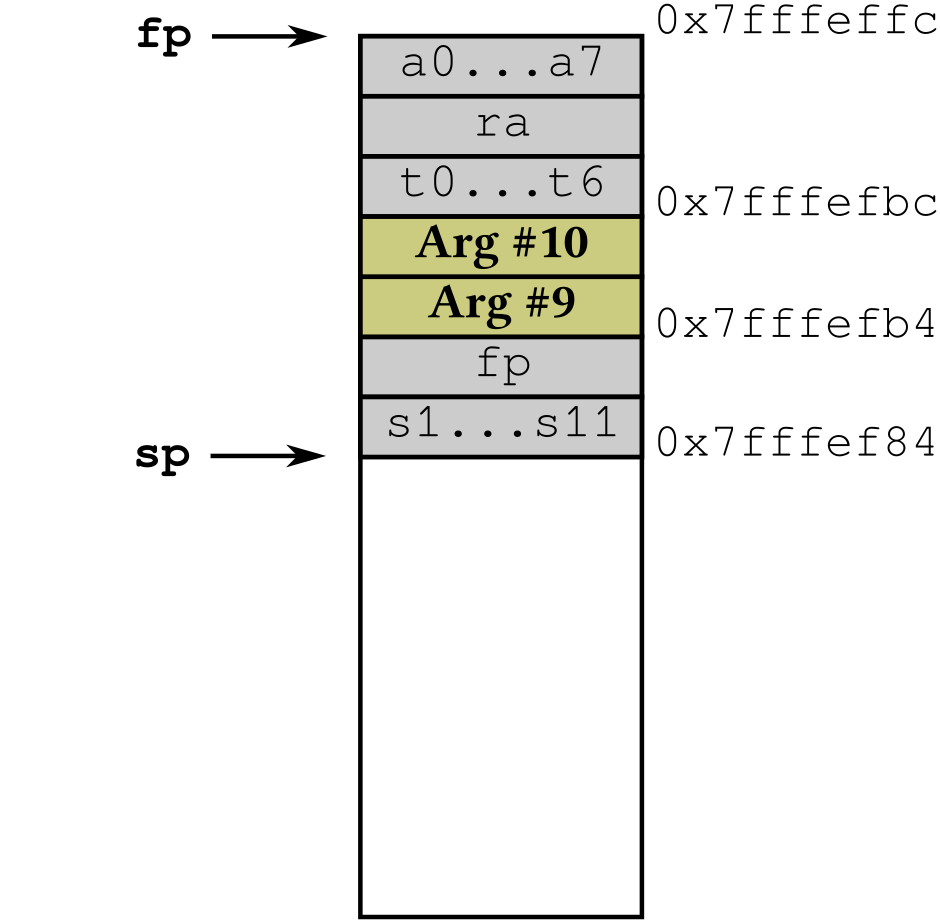
|
Next, the called function executes its prologue, which decreases the stack
pointer sp by 48 bytes to save its callee-saved registers. Such callee-saved
registers consist of:
the frame pointer
fp,the temporary registers
s1…s11,the stack pointer
sp— although we do not need to actually savespon the stack, because we can easily compute its old value later.
(For simplicity, here we are only considering integer registers, and we ignore
the fact the function f may not use use all registers between s1 and s11,
so saving all of them might not be necessary.)
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int, //<
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x0040103c
sp = 0x7fffef84
fp = 0x7ffff0b4
ra = 0x004000b0
a0 = 1
...
a7 = 8
t0 = 42
t1 = 0x00401000
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|
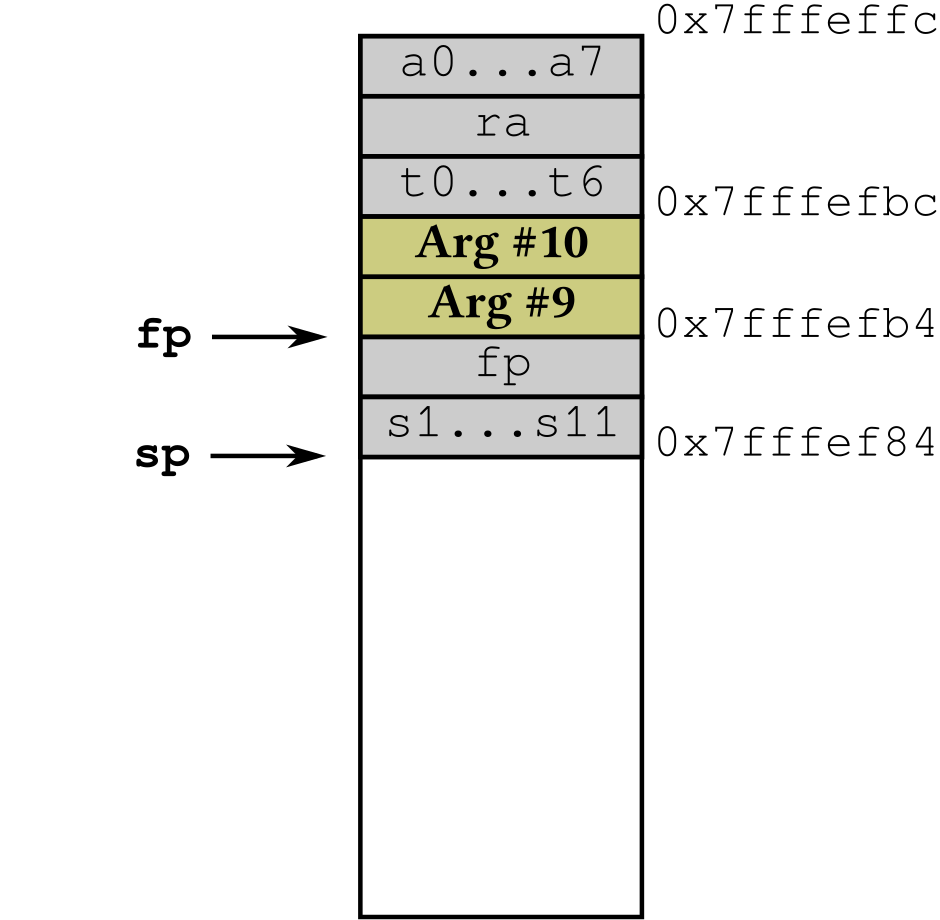
|
Then, the function prologue updates the frame pointer fp to the value of the
stack pointer sp before its last update (i.e. before the callee-saved
registers were saved on the stack): in this example, the frame pointer is set to
sp + 48.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10; //<
};
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x0040106c
sp = 0x7fffef84
fp = 0x7ffff0b4
ra = 0x004000b0
a0 = 1
...
a7 = 8
t0 = 87
t1 = 1
t2 = 2
...
t6 = 6
s1 = 7
...
s4 = 42
s5 = 42
...
|

|
Now, the body of the function begins its execution. To compute the sum, it will
load its arguments from registers r0…r7 and from the stack, and write the
result of their addition (which is 87) in the target register t0. As a
consequence, the values in registers t0…t6 and s1…s4 are
overwritten.
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10; //<
};
let x = 42;
let y = f(1,... 9, x);
print(x + y)
|
pc = 0x004010ac
sp = 0x7fffefb4
fp = 0x7fffeffc
ra = 0x004000b0
a0 = 87
...
a7 = 8
t0 = 87
t1 = 1
t2 = 2
...
t6 = 6
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
The function assembly code can now prepare for returning back to the caller, by executing the function epilogue, which performs the following steps:
it copies the result of the function body (available in its target register
t0) into the return value registera0;it restores all callee-saved registers to the values they had before the function was called:
it retrieves the old values of registers
fpands1…s11from the stack, andit restores the old value of
spby adding the number of restored registers multiplied by 4 (their size) to the current value ofsp(hence, by adding 12 * 4 = 48 to the current value offp).
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x)//<
print(x + y)
|
pc = 0x0040110c
sp = 0x7fffeffc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = 42
t1 = 87
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
Now the execution jumps back to the caller, i.e. to the address stored in
register ra — which is the first instruction after the function call. That
instruction is the beginning of the after-call assembly code, which:
copies the function’s return value from register
a0to the target register for the call (in this example,t1), andrestores all caller-saved registers excluding the target register
t1from the stack, andupdates the stack pointer by adding to the current value of
sp:the number of restored registers (16) multiplied by 4 (their size), and
the number of arguments passed on the stack (2) multiplied by 4 (their size).
Observe that now all registers are back to the same values they had before the
function call — with the exception of the program counter pc (which has
advanced to the current instruction) and the target register t1 (which
contains the return value of the function call).
Program |
Registers |
Stack |
|---|---|---|
fun f(x1: int,
...,
x10: int): int = {
x1 + ... + x10;
};
let x = 42;
let y = f(1,... 9, x);
print(x + y) //<
|
pc = 0x00401110
sp = 0x7fffeffc
fp = 0x7fffeffc
ra = ?
a0 = ?
...
a7 = ?
t0 = 42
t1 = 87
t2 = 1
...
t6 = 5
s1 = 6
...
s4 = 9
s5 = 42
...
|

|
The function call is now complete and the execution can continue regularly: the
code generation for the expression print(x, y) will find the values of
variables x and y in registers t0 and t1, respectively.
Implementation#
We now have a look at how hyggec is extended to implement function
instances (i.e. lambda terms) and applications, according to the specification
illustrated in the previous sections.
Tip
To see a summary of the changes described below, you can inspect the differences
in the hyggec Git repositories between the tags
while and functions.
Lexer, Parser, Interpreter, and Type Checking#
These parts of the hyggec compiler are extended along the lines of
Example: Extending Hygge0 and hyggec with a Subtraction Operator.
We extend
AST.fsin two ways, according to Definition 21:we extend the data type
Expr<'E,'T>with two new cases:Lambdafor “\(\hygLambda{x_1: t_1, \ldots, x_n: t_n}{e}\)”, andApplicationfor “\(\hygApp{e}{e_1,\ldots,e_n}\)”;
we also extend the data type
Pretypewith a new case calledTFun, corresponding to the new function pretype “\(\tFun{t_1, \ldots, t_n}{t}\)”:and Pretype = // ... /// A function pretype, with argument pretypes and return pretype. | TFun of args: List<PretypeNode> * ret: PretypeNode
We extend
PrettyPrinter.fsto support the new expressionsLambdaandApplication, and the new pretypeTFun.We extend
Lexer.fslto support three new tokens:FUNfor the new keyword “fun”;RARROW(right arrow) for the arrow “->” used to define lambda terms and function pretypes; andCOMMAfor the symbol “,” used to separate arguments in function instances, applications, and pretypes.Warning
If you have implemented
minandmaxas part of Project Idea (Easy): Extend Hygge0 and hyggec with New Arithmetic Operations, then you should have already introduced a token corresponding toCOMMA: you should reuse it (i.e. you should not have two tokens that match the same sequence of input characters).
We extend
Parser.fsyto recognise the desired sequences of tokens according to Definition 21, and generate AST nodes for the new expressions. We proceed by adding:a new rule under the
simpleExprcategory to generateLambdainstances;a new rule under the
unaryExprcategory to generateApplicationinstances;a new rule under the
pretypecategory to generateTFunpretype instances;various auxiliary syntactic categories and rules to recognise the syntactic elements needed by the rules above. For instance:
parenTypesSeqis a sequence of comma-separated pretypes, between parentheses (needed to parse function pretypes);parenArgTypesSeqis a sequence of comma-separated variables with type ascriptions, between parentheses (needed to parse the arguments of a lambda term);
finally, we also add a new rule to implement the syntactic sugar for simplified function definitions. To this purpose, we extend the
exprsyntactic category (because our simplified function definitions are just “let…” binders, so we want to give them the same precedence). The syntactic sugar rule looks as follows:expr: // ... | FUN ident parenArgTypesSeq COLON pretype EQ simpleExpr SEMI expr { let (_, args) = List.unzip $3 // Extract argument pretypes mkNode(..., Expr.Let($2, mkPretypeNode(..., Pretype.TFun(args, $5)), mkNode(..., Lambda($3, $7)), $9)) }
In other words, when the parser sees an expression like
fun f(x: int, y: int): int = x + 1, it creates aLetexpression instance that binds the variablef(with pretype(int, int) -> int) with the lambda termfun (x: int, x: int) -> x + 1(as expected by Definition 21).
We extend the function
substinASTUtil.fsto support the new expressionsLambdaandApplication, according to Definition 22.We extend
Interpreter.fsaccording to Definition 23:in the function
isValue, we add a new case forLambda(which is a value); andin the function
reduce:we add two new cases for
LambdaandApplication.
We extend
Type.fsby adding a new case to the data typeType, according to Definition 24: the new case is calledTFun. We also add a a corresponding new case to the functionfreeTypeVarsin the same file.Note
Correspondingly, we also extend the pretty-printing function
formatTypeinPrettyPrinter.fs, to display the function type we have just introduced.We extend
Typechecker.fs:we extend the type resolution function
resolvePretypewith a new case for function types, according to Definition 25;we extend the function
typeraccording to Definition 26, to support the new cases for the expressionsLambdaandApplication.
As usual, we add new tests for all compiler phases.
Code Generation#
This is certainly the trickiest part of the extension, because the RISC-V calling convention has many moving parts.
The extension of the function doCodegen (in the file Typechecker.fs)
consists of the following main elements (detailed in the following sections):
Code Generation for Lambda Terms#
We add a new case to the function doCodegen to handle Lambda expressions,
i.e. function instances. The key intuition is that, in order to turn a lambda
term into an actual RISC-V function, according to our discussion on
Code Generation for a Function Instance, we need to generate assembly code
to:
place a RISC-V assembly label to mark the memory address of the beginning of the function code: we will use that label to call the function;
generate code for the function prologue, to save the callee-saved registers and update the frame pointer;
generate code for the function body;
generate code for the function epilogue, to restore the caller-saved registers and copy the function result onto the return register
a0;make sure that all the function code is placed at the end of the assembly code generated by the
hyggeccompiler (because the execution starts from the beginning of the code, and we only want the function to run when it is called/applied);finally, place in the target register the memory address where the function is located (i.e. the label generated at point 1 above).
Note
As a consequence of points 1 and 5 above, the label and the assembly code of a
function instance are globally visible in the generated RISC-V assembly — even
when the original function instance was only visible in a limited scope (e.g.
like the function privateFun) in Example 35). To avoid
potential clashes, the compiler must ensure that the label assigned to each
function is unique across the generated assembly file.
The doCodegen case for Lambda looks as follows. (Note: the actual code on
the hyggec Git repository contain many more comments, and you should read it.)
let rec internal doCodegen (env: CodegenEnv) (node: TypedAST): Asm =
// ...
| Lambda(args, body) ->
let funLabel = Util.genSymbol "lambda" // Position of lambda term body
let (argNames, _) = List.unzip args // Names of lambda term arguments
// Pairs of arguments and types
let argNamesTypes = List.map (fun a -> (a, body.Env.Vars[a])) argNames
let bodyCode = compileFunction argNamesTypes body env // Body code
let funCode = // Complete function code, with label placed before it
Asm(RV.LABEL(funLabel), "Lambda function code")
++ bodyCode
.TextToPostText // Move this code at the end of the text segment
// Finally, load the function address (label) in the target register
Asm(RV.LA(Reg.r(env.Target), funLabel), "Load lambda function address")
++ funCode
Steps 2, 3, and 4 are handled by the auxiliary function compileFunction: its
code is not reported here, but it has plenty of comments: you should read it to
see what it does.
Exercise 30 (Understanding Code Generation for Function Instances)
Write a file called e.g. fun.hyg containing a simple function instance, such
as:
fun (x: int, y: int) -> x + y
Invoke ./hyggec compile fun.hyg and observe the generated assembly. Using the
comments in the generated assembly, identify the corresponding parts of the
functions doCodegen (case for Lambda) and compileFunction.
Warning
The code of compileFunction is very limited, because:
it only supports functions that take up to 8 arguments, passed via integer registers; and
it only supports functions that return their value through an integer register; and
in addition, it has the overall limitations that we discuss later.
Some of the missing features (e.g. taking more than 8 integer arguments, taking and returning float values) are part of the Project Ideas for this module.
Code Generation for Named Functions#
The Code Generation for Lambda Terms (described above) assigns a random label to the mark the location of the function’s compiled assembly code. This is not an issue for lambda terms, which are anonymous. However, Hygge programs may define functions by giving them a specific immutable name, e.g. by using the syntactic sugar:
fun add(x: int, y: int): int = x + y;
add(1, 2)
which expands into:
let add: (int, int) -> int =
fun (x: int, y: int) ->
x + y;
add(1, 2)
The function doCodegen includes a dedicated case that matches such “let…”
bindings that directly use a lambda term to initialise an immutable variable.
In this case, hyggec performs code generation as follows:
it uses the name of the variable to generate a label in the assembly code. That label is placed at the beginning of the assembly code of the function; and
when assigning storage information, it maps the variable directly to the assembly label above (instead, the standard code generation for “let…” would store the variable in a register, hence it would use one additional register).
The code for this case of doCodegen looks as follows (and it is essentially a
blend between the case for Let and the
Code Generation for Lambda Terms):
let rec internal doCodegen (env: CodegenEnv) (node: TypedAST): Asm =
// ...
| Let(name, {Node.Expr = Lambda(args, body);
Node.Type = TFun(targs, _)}, scope)
| LetT(name, _, {Node.Expr = Lambda(args, body);
Node.Type = TFun(targs, _)}, scope) ->
let funLabel = Util.genSymbol $"fun_%s{name}" // Function label
let (argNames, _) = List.unzip args // Names of lambda term arguments
let argNamesTypes = List.zip argNames targs // Pairs or argument & type
let bodyCode = compileFunction argNamesTypes body env // Compiled body
let funCode = // Compiled function code, with label placed in front
(Asm(RV.LABEL(funLabel), $"Code for function '%s{name}'")
++ bodyCode).TextToPostText
/// Storage info with name of compiled function pointing to 'funLabel'
let varStorage2 = env.VarStorage.Add(name, Storage.Label(funLabel))
// Compile the 'let...'' scope with newly-defined function visible
(doCodegen {env with VarStorage = varStorage2} scope)
++ funCode
Exercise 31 (Understanding Code Generation for Named Functions)
Write a file called e.g. fun-named.hyg containing a simple named function
instance, such as:
fun add(x: int, y: int): int = x + y;
()
Invoke ./hyggec compile fun-named.hyg and observe the generated assembly.
Notice the difference with Exercise 30. Using the
comments in the generated assembly, identify the corresponding parts of the
functions doCodegen (case for Let with lambda terms) and compileFunction.
Code Generation for Applications#
We add a new case to the function doCodegen to handle Application
expressions, i.e. function calls. The key intuition is that, in order to turn
an application into an actual RISC-V function call, according to our discussion
on Code Generation for a Function Call, we need to generate assembly code
to:
compute the term being applied as a function (e.g. retrieve the memory address of the function being applied);
compute each argument of the function call;
perform the “before-call” procedures: save the caller-saved registers, and prepare the function arguments (by copying them onto the ‘a’ registers or on the stack);
perform the function call; and
perform the “after-call” procedures: copy the function call result from the return register
a0onto the target register of the call.
The doCodegen case for Application looks as follows. (Note: the actual code
on the hyggec Git repository contain many more details and comments, and you
should read it!)
let rec internal doCodegen (env: CodegenEnv) (node: TypedAST): Asm =
// ...
| Application(expr, args) ->
let saveRegs = // ...Saved registers (except the target register)
let appTermCode = // ...Code for expression being applied
let argsCode = // ...Generate code to compute each application argument
let argsLoadCode = // ...Copy each application arg into an 'a' register
let callCode = // Code that performs the function call
appTermCode
++ argsCode // Code to compute each argument of the function call
.AddText(RV.COMMENT("Before call: save caller-saved registers"))
++ (saveRegisters saveRegs [])
++ argsLoadCode // Code to load arg values into arg registers
.AddText(RV.JALR(Reg.ra, Imm12(0), Reg.r(env.Target)), "Call")
let retCode = // Code that handles the function return value (if any)
Asm(RV.MV(Reg.r(env.Target), Reg.a0),
$"Copy function return value to target register")
callCode // Put everything together, restore the caller-saved registers
.AddText(RV.COMMENT("After function call"))
++ retCode
.AddText(RV.COMMENT("Restore caller-saved registers"))
++ (restoreRegisters saveRegs [])
Exercise 32 (Understanding Code Generation for Function Application)
This is a follow-up to Exercise 30 and
Exercise 31. Write a file called e.g.
fun-app.hyg containing a simple function instance and application, such as:
(fun (x: int, y: int) -> x + y)(1, 2)
Invoke ./hyggec compile fun-app.hyg and observe the generated assembly. Using
the comments in the generated assembly, identify the corresponding parts of the
functions doCodegen (case for Application).
Now try a similar experiment on a file with a corresponding named function definition and application, such as:
fun add(x: int, y: int): int = x + y;
add(1, 2)
Observe the differences with the assembly code generated in the previous case.
Warning
The code generation for Application expressions is very limited, because:
it only supports functions that take up to 8 arguments, passed via integer registers; and
it only supports functions that return their value through an integer register; and
in addition, it has the overall limitations that we discuss later.
Some of the missing features (e.g. passing more than 8 integer arguments, passing and returning float values) are part of the Project Ideas for this module.
Limitations of the Current Specification and Code Generation#
To conclude, we highlight that the treatment of functions presented in this module has relevant limitations in the support for closures, i.e. lambda terms that capture variables from their surrounding scope. Here is a simple program with a closure:
let x = 1;
fun addX(y: int): int = y + x; // x is captured from the surrounding scope
assert(addX(42) = 43)
In particular:
the Code Generation does not support closures at all, and the code generation for examples like the one above is incorrect;
the Operational Semantics and Typing Rules correctly support closures for immutable variables (like in the example above), but do not correctly support closures for mutable variables. As a consequence, a well-typed program that captures mutable variables may get stuck!
These limitations require further improvements of the Hygge language and
hyggec compiler: we will address them later in the course.
References and Further Readings#
The treatment of lambda terms, applications, and function types in Hygge is inspired by languages with functional programming support (like Java 8 or higher, Kotlin, F#, Scala, Haskell…), and its specification based on programming language theory concepts. To know more, you can refer to:
Benjamin Pierce. Types and Programming Languages. MIT Press, 2002. Available on DTU Findit. These chapters, in particular, may be useful:
Chapter 5 (The Untyped Lambda-Calculus)
Chapter 9 (Simply Typed Lambda-Calculus)
The RISC-V calling convention is documented here:
Note
For simplicity, in this module we have omitted a requirement of the RISC-V
calling convention: the frame pointer address should always be aligned to 16
bytes (128 bits). This requirement is not enforced by RARS — but when
targeting real RISC-V hardware, hyggec (or any other compiler) should keep
track of the alignment of register fp and always increase/decrease it by
multiples of 16 bytes.
Project Ideas#
Here are some ideas for your group project.
Project Idea (Medium Difficulty): Function Subtyping#
The extensions described in this module does not change the subtyping judgement (Definition 10). As a consequence, whenever two function types are compared to see whether one is subtype of the other, the only applicable rule is \(\ruleFmt{TSub-Refl}\), which requires the two types to be exactly equal. This leads to the restriction illustrated in Example 41 below.
Example 41 (Consequences of Lack of Function Subtyping)
The following program does not type-check: you can see it by
yourself, by saving this program in a file and running
./hyggec typecheck file.hyg.
type MyInt = int;
fun f(x: MyInt): MyInt = x + 1; // Type error!
let fAlias: (int) -> int = f; // Type error!
assert(fAlias(42) = f(42))
The reasons for the type errors reported by hyggec are the following:
when defining
f, the function should be of type(MyInt) -> MyInt, but its definition has type(MyInt) -> int(because the expressionx + 1has typeint, instead ofMyInt);when defining
fAlias, the initialisation value should be a function of type(int) -> int, butfhas type(MyInt) -> MyInt.
These type errors certainly feel spurious: since MyInt is just an alias of
int, those function types should be all subtypes of each other! And indeed,
if we interpret the program above (using ./hyggec interpret file.hyg), the
program runs correctly and passes the assertion (in fact, there is a test case
for the hyggec interpreter that corresponds to this example).
For this Project Idea, you should extend hyggec with function subtyping,
by adding the following rule to Definition 10:
Recall that, by the Liskov Substitution Principle (Definition 9), an instance of a subtype should be safely usable whenever an instance of a larger type is required. Correspondingly rule \(\ruleFmt{TSub-Fun}\) above says that a function type \(\tFun{T_1, \ldots, T_n}{T}\) is subtype of \(\tFun{T'_1, \ldots, T'_n}{T'}\) if:
both function types expect \(n\) arguments;
for all \(i \in 1..n\), the argument type \(T'_i\) is subtype of the corresponding argument type \(T_i\) (in other words, the “smaller” function is more permissive in the types of arguments it accepts); and
the return type \(T\) is subtype of the return type \(T'\) (in other words, the “smaller” function is more restrictive in the type of value it returns).
To extend hyggec with function subtyping, you will need to:
extend the function
isSubtypeOfin the fileTypechecker.fs; andadd some test cases that would not type-check without function subtyping (e.g. using Example 41 as a starging point). Your tests should include functions that take other functions as arguments, and functions that return functions, as in Example 35.
Note
If you choose this Project Idea, you will also need to add more test cases that show how function subtyping interplays with structure subtyping, and union subtyping (addressed later in the course).
Project Idea (Hard): Recursive Functions#
The goal of this Project Idea is to allow a function to call itself recursively. To this end, you should:
extend the Hygge programming language with a “let rec…” expression, similar to F# (and similar to the existing “let…” for immutable variables); and
you should add syntactic sugar for
rec fun name(...)...inParser.fsyto expand into a “let rec…” expression (instead of the regular “let…”).
More in detail, you will need to implement the following specification.
First, you need to add a new expression to the Hygge syntax (notice that this
introduces a new token for the symbol rec).
You will need to add a new LetRec expression in AST.fs, similar to Let.
You will also need to add a rule to parse the syntactic sugar
rec fun name(...):... = ... in Parser.fsy: the new parsing rule should
create a LetRec AST node that initialises the variable name with a lambda
term with the function body. This way, it becomes possible for a Hygge
programmer to write a named function that calls itself recursively.
Then, you will need to implement the substitutions and the semantic rules for the new “let rec…” expression. For substitution, you need to add these new cases to Definition 2:
There is only one difference between the substitution above and the substitution for the regular “let \(x\)…” (Definition 2): in the first case above (i.e. when we substitute a variable \(x\) that has the same name of the variable bound by “let rec \(x\)…”), the substitution has no effect (instead, in the regular “let \(x\)…” we propagate the substitution in the initialisation expression of \(x\)). The reason is that in “let rec \(x\)…”, the variable \(x\) is visible and bound in the initialisation expression, hence we “block” its substitution.
For the “let rec…” semantics, you need to add the following rules to Definition 4:
The difference between rule \(\ruleFmt{R-Let-Subst}\) (in Definition 4) and rule \(\ruleFmt{R-LetRec-Subst}\) above is that:
in rule \(\ruleFmt{R-Let-Subst}\), the variable being defined (\(x\)) is replaced by the initialisation value \(v\) in the scope of the “let…” expression;
instead, in rule \(\ruleFmt{R-LetRec-Subst}\), the variable being defined (\(x\)) is replaced by \(v'\), which is obtained by taking the initialisation value \(v\) and replacing each occurrence of \(x\) within \(v\) with an instance of \(\hygLetRec{x}{t}{v}{x}\). Notice that this substitution can only have an effect when \(v\) is a lambda term that contains instances of \(x\). (See Example 42 below.)
Then, you will need to implement the following typing rule for the new “let rec…” expression:
The new typing rule \(\ruleFmt{T-LetRec}\) above is similar to rule \(\ruleFmt{T-Let-T2}\) in Definition 16, except that:
in rule \(\ruleFmt{T-Let-T2}\), the initialisation expression for the variable \(x\) is typed with the typing environment \(\Gamma\). As a consequence, \(e_1\) cannot refer to the same variable \(x\) being defined by the “let…” expression;
instead, in rule \(\ruleFmt{T-RetLec}\) above, the initialisation expression for the variable \(x\) is typed with the extended typing environment \(\Gamma'\), which includes the type of \(x\) (and the same \(\Gamma'\) is also used to type \(e_2\)). As a consequence, \(e_1\) can be well-typed even if it recursively refers to \(x\), i.e. the variable being defined by the “let rec…”;
moreover, in rule \(\ruleFmt{T-RetLec}\) above, the initialisation expression for the variable \(x\) can only be a lambda term \(\hygLambda{x_1: t_1, \ldots}{e_1}\) (and consequently, its type \(T\) can only be a function type).
Finally, you will need to extend doCodegen (in RISCVCodegen.fs) for
compiling the new LetRec expression. You can focus on adding a new special
case for compiling recursive functions with a given immutable name (which are
generated by the new syntactic sugar rec fun name(...)...): this special case
should be similar to the existing analogous special case for the code generation
of Let, which maps the storage of name to an assembly label. The difference
is that:
the new special case should match a
LetRecexpression (instead ofLet), andthe new special case should compile the
initialisation expression of theLetRecby making the functionnameavailable viaenv.VarStorage(this way, theinitexpression can recursively call the function being compiled).
As usual, you should write tests for all the compiler phases you modified.
Note
The new typing rule \(\ruleFmt{T-LetRec}\) above constraints the initialisation expression to be a lambda term to disallow invalid recursive definitions like “\(\hygLetRec{x}{t}{x}{\ldots}\)”. Such invalid definitions are also rejected e.g. by the F# type checker (try it!).
Example 42 (Reductions of a Recursive Function)
Consider the following Hygge program, where function \(f\) calls itself:
Intuitively, this expression should execute forever by calling \(\hygApp{f}{0}\), then \(\hygApp{f}{0+1}\), then \(\hygApp{f}{1+1}\)…
According to this Project Idea, the expression above should desugar the function definition into a “let rec…” expression:
If we reduce this expression in a runtime environment \(R\), using the new rule \(\ruleFmt{R-LetRec-Subst}\), we get:
The next reduction performs the top-level function application:
We now have another application, and we need to reduce the expression being applied into a value. To this end, we use rule \(\ruleFmt{R-LetRec-Subst}\) again:
We now need to reduce the application argument into a value:
And by performing the application, we get:
Observe that this last reduction produced an expression that is very similar to the one we obtained with the first use of rule \(\ruleFmt{R-App-Res}\) above — except that the first time we obtained an application of “let rec…” to \((0+1)\), while now we have obtained an application of the same “let rec…” to \((1+1)\). Therefore, we can continue reducing forever, and every time we will obtain an application of the same “let rec…” to a bigger value.
Project Idea (Medium Difficulty): Improved Implementation of the RISC-V Calling Convention: Pass and Return Floats via Registers#
The goal of this Project Idea is to extend hyggec to support functions that
receive floating-point arguments, or return a floating-point value. To this
end, you should follow The RISC-V Calling Convention and Its Code Generation, and improve the
hyggec Code Generation. Note that your extension
should support function that receive a mix of integer and float arguments, in
any order, such as:
fun f(w: int, x: float, y: bool, z: string): float = {
if y then println(z) else println(w+1);
x + 42.0f
};
println(f(2, 1.0f, true, "Hello"));
println(f(2, 2.0f, false, "Hello"))
Project Idea (Hard): Improved Implementation of the RISC-V Calling Convention: Pass more than 8 Integer (or Float) Arguments via The Stack#
The goal of this Project Idea is to extend hyggec to support functions that
receive more that 8 integer arguments, by passing the arguments above the 8th on
the stack. To this end, you should follow
The RISC-V Calling Convention and Its Code Generation, and improve the hyggec
Code Generation.
Hint
To implement this project idea, you will need to extend the type Storage in
RISCVCodegen.fs with a new case, describing a variable that can be found on
the stack. The new case for Storage may look as follows:
type internal Storage =
// ...
/// This variable is stored on the stack, at the given offset (in bytes)
/// from the memory address contained in the frame pointer (fp) register.
| Frame of offset: int
Note
If you have also selected the Project Idea on passing/returning floats, keep in mind that what you should pass on the stack are:
all integer arguments above the 8th integer argument, and
all float arguments above the 8th float argument.
As a consequence, a call to the following function should not pass any argument via the stack:
fun f(x1: int, x2: int, x3: int, x4: int, x5: int,
y1: float, y2: float, y3: float, y4: float, y5: float): bool = {
// ...
}
//...
This is because, although f has 10 arguments in total, it takes less than 9
integer arguments, and less than 9 float arguments.

