Module 3: Hands-On with hyggec#

This module outlines the implementation of the hyggec compiler, in its minimal version that implements the Hygge0 programming language specification. We explore how hyggec works, and how it translates a Hygge0 program into corresponding RISC-V code. We see how to extend both the Hygge0 language and the hyggec compiler with new features. We conclude this module with some Project Ideas.

Important

This module introduces quite a lot of information that you will use throughout the rest of the course, while working on your project.

Here is a recommendation:

  • first, focus on grasping the overall picture of how hyggec works, without trying to memorise every detail;

  • then, use this module as a reference: come back here when you will need to investigate some aspect of the hyggec compiler in more detail. While working on the project, you will also become more familiar with the hyggec internals.

Quick Start#

  1. Go to the hyggec Git repository: https://gitlab.gbar.dtu.dk/02247/f24/hyggec (NOTE: you will need to log in with your DTU account)

  2. Create your own fork of the repository, by clicking on the “Fork” button (to the right of the hyggec title and logo)

    Important

    To avoid possible plagiarism issues, make sure your forked repository is private, and only accessible by you and your team members. You can configure the repository access on the forked repository page, on the menu to the left, by clicking “Project information” → “Members”.

  3. Clone your forked repository on your computer (use the “Clone” button to the right. You may choose between “HTTPS” or “SSH”, and the latter is probably better; you may need to configure your SSH keys for authenticating)

  4. Follow the instructions in the file README.md in the hyggec repository.

Important

  • The hyggec Git repository linked above will be updated during the course with the new features presented in each Module. Each feature update will have a separate Git tag to distinguish it. The instructions in this Module refer to the hyggec code up to the tag hygge0.

  • If you want, you can find all the hyggec compiler updates (covering the whole course) in the “full” Git repository: https://gitlab.gbar.dtu.dk/02247/f24/hyggec-full. Both the hyggec and hyggec-full repositories will have the same Git history and tags: the teacher will progressively push the changes from hyggec-full into the hyggec repository. You may decide to work on your project by directly cloning (or pulling changes from) the hyggec-full repository: this may help minimising merge conflicts with your project work during the course. The drawback is that the hyggec-full repository contains code that will be explained later in the course, and may be initially unclear.

The Compiler Phases of hyggec#

In the beginning of the course, we discussed what is a compiler and what are the typical phases that allow a compiler to translate an input program into an output program.

hyggec has the same phases illustrated in Fig. 2. In this section we explore how each phase is implemented. The overall picture is illustrated in Fig. 3, where:

  • each compiler phase is annotated with the file that handles it in hyggec, and

  • each intermediate compilation product is annotated with the data type that hyggec uses to represent it.

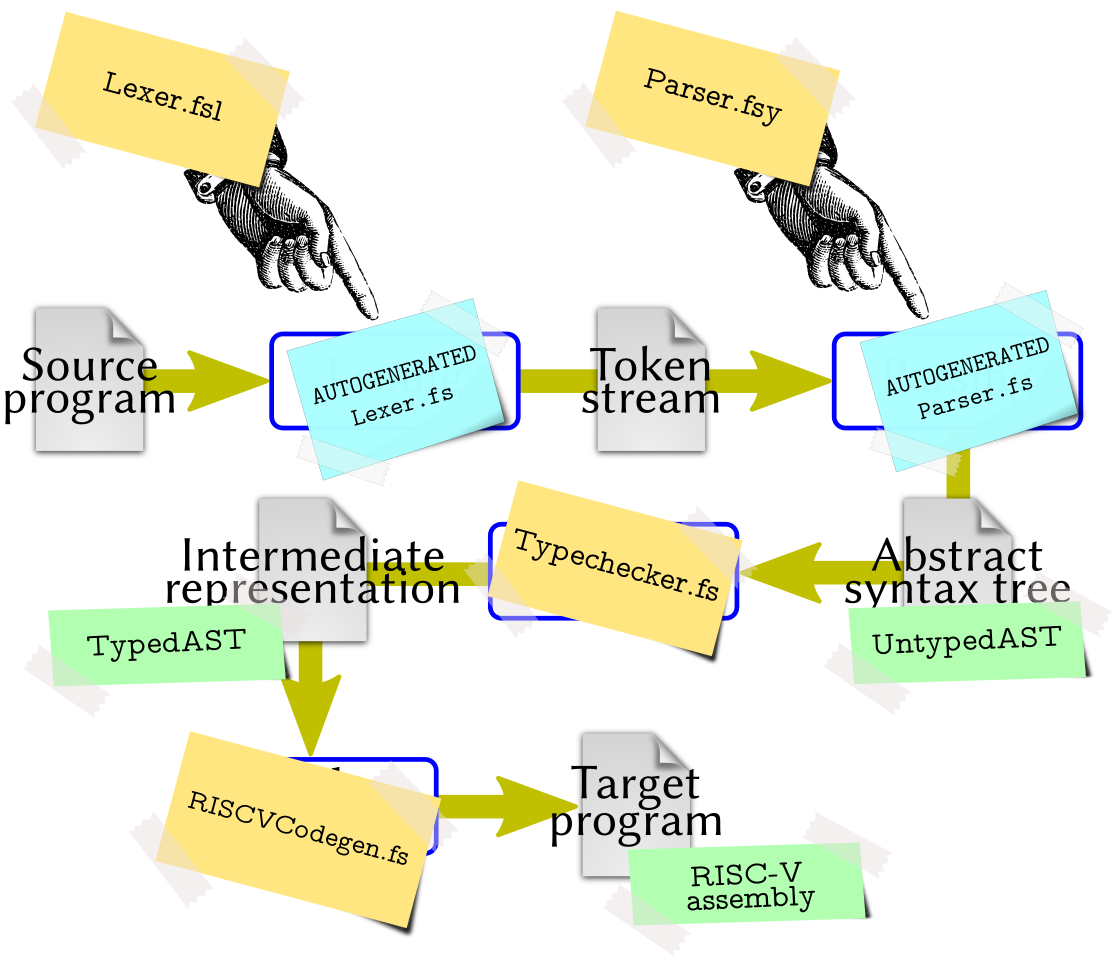
Diagram of the `hyggec` compiler phases

Fig. 3 Phases of the hyggec compiler (diagram based on Fig. 2).#

Overview of the hyggec Source Tree#

Here is a quick summary of the hyggec source code structure: the files and directories are roughly ordered depending on how soon (and how often) you will use or modify them.

Tip

When exploring the hyggec source code with Visual Studio Code (or similar IDEs), try to hover with the mouse pointer on types, function names, and variables: in most cases, you will see a brief description of their purpose (and you can jump to their definition, if you want).

Table 4 Overview of the hyggec source tree.#

File or directory name

Description

hyggec and hyggec.bat

Scripts to run hyggec on Unix-like and Windows operating systems. Both scripts cause the automatic recompilation of hyggec if its source code was changed after the last run.

src/

Directory containing the hyggec source files.

tests/

Directory containing the hyggec test suite. We discuss the structure of its subdirectories in The Test Suite of hyggec.

src/AST.fs

Representation of the Abstract Syntax Tree (AST) of Hygge0, based on the Definition 1. This file is discussed below in The Abstract Syntax Tree.

src/ASTUtil.fs

Utility functions for manipulating an AST (e.g. apply substitutions).

src/Lexer.fsl and src/Parser.fsy

Specification of the lexer and parser that read Hygge0 source code files and build the corresponding AST. These files are discussed below in The Lexer and Parser.

src/Interpreter.fs

Interpreter for Hygge programs, based on the Structural Operational Semantics of Hygge0.

src/Type.fs

Definition of Hygge0 types (based on Definition 5).

src/Typechecker.fs

Functions for performing type checking on a given Hygge0 program AST, according to Definition 8 and Definition 11 (thus including Subtyping).

src/RISCVCodegen.fs

Functions for generating RISC-V assembly code from a well-typed Hygge0 program AST.

src/RISCV.fs

Functions for creating and manipulating RISC-V assembly code fragments.

src/PrettyPrinter.fs

Functions to pretty-print various compiler data structures (e.g. ASTs or typing environments)

src/Log.fs

Utility functions for logging messages on the console.

src/Util.fs

Miscellaneous utility functions (e.g. for generating unique strings or numbers).

src/CmdLine.fs

Configuration of the hyggec command line options.

src/Program.fs

The main program, with the main function.

examples/

This directory contains a few examples of Hygge0 programs.

src/Test.fs

Test suite configuration and execution functions. The test suite uses the Expecto testing library.

hyggec.fsproj

.NET project file.

src/RARS.fs

Utility functions to launch RARS — RISC-V Assembler and Runtime Simulator and immediately execute the compiled RISC-V assembly code.

lib/

This directory contains a copy of RARS — RISC-V Assembler and Runtime Simulator, used in RARS.fs (see above).

rars and rars.bat

Scripts to launch RARS on Unix-based and Windows operating systems. These scripts use the copy or RARS contained in the lib/ directory.

README.md and LICENSE.md

Should be self-explanatory…

fsharplint.json

Configuration file for FSharpLint (you can ignore it).

src/Parser.fs, src/Parser.fsi, src/Lexer.fs, src/Lexer.fsi

Auto-generated parser and lexer files, overwritten when the hyggec source is recompiled. Do not edit these files!

bin/ and obj/

Auto-generated directories, overwritten when the hyggec source is recompiled. Do not edit the contents of these directories!

The Abstract Syntax Tree#

After the specification of a programming language is completed, one of the first steps towards developing a compiler is (typically) defining the data structures needed for the internal representation of a syntactically-correct program, after it has been read from an input file. This internal representation is called Abstract Syntax Tree (AST) (where the term “abstract” differentiates it from the concrete syntax tree handled by the parser, that we discuss later). The AST definition follows the grammar of the language being compiled, with possible adjustments for simplifying the overall compiler implementation.

In the case of hyggec, the AST is defined in the file src/AST.fs and is based on the Hygge0 grammar in Definition 1. However, the AST definition includes some adjustments, that we now illustrate.

Defining the AST: First Attempt#

In a programming language like F#, we can very naturally specify an AST using discriminated unions. For instance, we can:

  1. define a type Expr for representing a generic Hygge0 expression \(e\), with a dedicated named case to represent each different kind of expression in Definition 1; and

  2. in each named case, use fields of type Expr for representing sub-expressions.

For example, starting from the bottom of Definition 1, we may define our AST type Expr as:

type Expr =
    | UnitVal                  // Unit value
    | BoolVal of value: bool   // Boolean value
    | IntVal of value: int     // Integer value
    // ...
    | Var of name: string      // Variable

    // Addition between left-hand-side and right-hand-side sub-expressions.
    | Add of lhs: Expr
           * rhs: Expr

    // Multiplication between left-hand-side and right-hand-side sub-expressions.
    | Mult of lhs: Expr
            * rhs: Expr

    // ...

Using the type definition above, the Hygge0 expression “\(42 + x\)” would be represented in F# as:

Add( IntVal(42), Var("x") )

This approach is valid, but it has two drawbacks.

  1. The definition of Expr above does not include information about the position (line and column number) of each sub-expression in the original input file being compiled. We will need this information to generate helpful error messages during type checking, to help Hygge0 programmers find and fix errors in their programs.

  2. During type checking, we take a Hygge0 expression \(e\) and compute its typing derivation by following the syntactic structure of \(e\). Therefore, the typing derivation of \(e\) has pretty much the same shape of the syntax tree of \(e\): see, for instance, the typing derivations in Example 14 and Example 15. The main difference is that, unlike a syntax tree, a typing derivation includes information about:

    • the type assigned to each sub-expression, and

    • the typing environment used to assign such a type.

    This information will be necessary for code generation, so it is very convenient to save it somewhere, when it is generated during type checking. And given the similarities between an AST and a typing derivation, it would be nice to somehow represent both of them with the same data type, thus avoiding code duplication.

The AST Definition#

We address both drawbacks discussed above in the final definition of the Hygge0 AST, which is available in the file src/AST.fs. The key idea is that we “wrap” each Expr object with a record of type Node (representing a node of the AST) which includes:

  1. the position of the expression in the original source file, and

  2. information about the typing of the expression. This information is absent before type-checking, and becomes available after type-checking.

As a result, we obtain a unified data type that includes the position of each expression, and can represent ASTs both before and after they are type-checked. This approach is adopted by many compilers (although the details may vary depending on the implementation programming language); the design here is inspired by the Scala 3 compiler.

The final definition of AST Nodes and Expressions in hyggec is the following.

type Node<'E,'T> = 
    {
      Expr: Expr<'E,'T> // Hygge expression contained in this AST node
      Pos: Position     // Position of the expression in the input source file
      Env: 'E           // Typing environment used to type-check the expression
      Type: 'T          // Type assigned to the expression
    }

and Expr<'E,'T> =
    | UnitVal                  // Unit value
    | BoolVal of value: bool   // Boolean value
    | IntVal of value: int     // Integer value
    // ...
    | Var of name: string      // Variable

    // Addition between left-hand-side and right-hand-side sub-expressions.
    | Add of lhs: Node<'E,'T>
           * rhs: Node<'E,'T>

    // Multiplication between left-hand-side and right-hand-side sub-expressions.
    | Mult of lhs: Node<'E,'T>
            * rhs: Node<'E,'T>

    // ...

The two type arguments of Node<'E,'T> and Expr<'E,'T> are used as follows:

  • 'E specifies what typing environment information is associated to each expression in the AST;

  • 'T specifies what type information is assigned to each expression in the AST.

The hyggec compiler handles two kinds of ASTs, both based on the definition of Node<'E,'T> above:

  • UntypedAST, which contains expressions of type UntypedExpr (both defined in src/AST.fs). UntypedAST and UntypedExpr are just type aliases, respectively, for Node<unit, unit> and Expr<unit, unit>: they represent AST nodes and expressions without any information (unit) about their typing environments or types (see Example 18 below). This kind of AST represents a syntactically-valid Hygge0 expression read from an input file; it is produced by The Lexer and Parser, and it may contain expressions that get stuck, like the ones discussed in Example 13.

  • TypedAST, which contains expressions of type TypedExpr (both defined in src/Typechecker.fs). TypedAST and TypedExpr are just type aliases, respectively, for Node<TypingEnv, Type> and Expr<TypingEnv, Type>: they represent AST nodes and expressions that have been type-checked, and have typing information available (similarly to a typing derivation). We discuss TypedASTs in Types and Type Checking.

Example 18 (Untyped AST of a Hygge0 Expression)

Consider the Hygge0 expression “\(42 + x\)”. Its representation in F# as an instance of type UntypedAST (i.e. Node<unit, unit>) is the following:

{
    Pos  = ... // Position in the input source file
    Env  = ()
    Type = ()
    Expr = Add( {
                    Pos  = ... // Position in the input source file
                    Env  = ()
                    Type = ()
                    Expr = IntVal(42)
                },
                {
                    Pos  = ... // Position in the input source file
                    Env  = ()
                    Type = ()
                    Expr = Var("x")
                } )
}

The file src/AST.fs also defines two types called PretypeNode and Pretype that represent, respectively, the syntax tree node of a pretype, and the pretype itself from Definition 1.

type PretypeNode =
    {
      Pos: Position    // Position of the pretype in the source file
      Pretype: Pretype // Pretype contained in this Abstract Syntax Tree node
    }

and Pretype =
    | TId of id: string  // A type identifier

Note

This representation of pretypes with two data types may seem a bit redundant — but it will allow us to easily extend the Pretype definition (and the types supported by hyggec) later in the course.

The Lexer and Parser#

After we establish the internal representation of the AST, a logical next step in constructing a compiler is to develop the functions that builds such ASTs by reading some input text (i.e. the source code we wish to compile). To this purpose, we need to develop two components.

  • A lexer (a.k.a. tokenizer or scanner) that reads the input text and classifies groups of characters that are either “useful” for building a syntax tree (e.g. identifiers, operators, parentheses…) or “useless” (e.g. sequences of white spaces, newlines, comments…). These groups of characters are typically recognised by matching them against a set of regular expressions; the goal of the lexer is to discard useless groups of characters, and turn the useful groups into tokens (or lexemes): each token captures a group of character and assigns to it a lexical category. The lexer should also report a tokenization error if it sees a sequence of input characters that it cannot classify.

  • A parser that reads a stream of tokens produced by a lexer, and tries to match them against a set of grammar rules, thus producing a corresponding syntax tree. The parser should produce a syntax error if it is unable to match the input tokens with any of the grammar rules.

Building lexers and parsers is typically a routine job (unless the programming language we wish to parse has a peculiar syntax…), and is also very time-consuming. For these reasons, there exists a wide variety of tools called lexer generators and parser generators — i.e. programs that:

  1. read a configuration file containing a specification of the language we wish to parse (as a description of its tokens and/or grammar rules, similar to Definition 1); and

  2. generate the source code of a lexer and/or parser, based on such a configuration file. The generated code can then be included and used as part of a compiler.

Here are some examples of lexer and parser generators.

  • Lex and Yacc are standard tools for generating lexers/parser in C, available on all Unix-like operating systems. These tools were initially released in the 1970s!

  • Flex and GNU Bison are more modern, improved replacements for Lex and Yacc.

  • FsLex and FsYacc are a lexer and parser generator for F#: they are used in hyggec.

  • ANTLR can generate lexers/parsers in various programming languages, and is especially popular in the Java world.

In the following sections we focus on FsLex and FsYacc, and how they are used in hyggec: after an overview of their respective configuration files (Parser.fsy and Lexer.fsl), we discuss an example showing the lexer and parser in action.

The Parser Configuration File Parser.fsy (Simplified)#

The file Parser.fsy is a configuration file for the FsYacc parser generator. This file specifies the rules for transforming a sequence of tokens (obtained from the lexer, discussed below) into an AST.

The file Parser.fsy has the following structure: here we see a very simplified fragment that only accepts additions between integers and variables. (We will discuss about these simplifications again later, in The Real Parser.fsy).

 1%{
 2// Preamble with definitions of types and/or functions.  The code appearing here
 3// will be placed on top of the generated parser source code.
 4
 5// Auxiliary function to build an untyped AST node for a Hygge expression.
 6let mkNode (..., expr: UntypedExpr) : UntypedAST = // ...
 7%}
 8
 9// Name of the grammar rule (defined below) to parse first.
10%start program
11
12// Declaration of tokens (values, operators, ...).  These tokens are recognised
13// by the lexer according to its configuration in Lexer.fsl.
14%token <int> LIT_INT
15%token PLUS
16// ...
17
18%token <string> IDENT // Generic identifier (might be a variable, pretype, etc.)
19%token EOF // Signals the End-Of-File
20
21%%
22
23// After '%%' above, we specify the rules of the grammar.  When a rule matches,
24// it produces a value, which is computed by running the snippet of F# code next
25// to the rule itself (between curly brackets).  The snippet of code, in turn,
26// can use the values produced when matching each symbol in its own rule, by
27// referring to the symbol position in the rule ($1, $2, ...).
28
29// Starting point: parsing rule for a whole Hygge program.
30program:
31    | expr EOF  { $1 } // A program is an expression followed by End-Of-File
32
33expr:
34    | expr PLUS expr  { mkNode(..., Expr.Add($1, $3)) }
35    | value           { mkNode(..., Expr.IntVal($1)) }
36    | variable        { mkNode(..., Expr.Var($1)) }
37    // ...
38
39value:
40    | LIT_INT  { $1 } // We just return the integer captured by token 'LIT_INT'
41    // ...
42
43variable:
44    | ident    { $1 }
45
46ident:
47    | IDENT    { $1 } // We just return the string captured by the token 'IDENT'

The parser configuration above declares, on lines 14–19, a few tokens:

  • LIT_INT (literal integer), which also carries an integer value;

  • PLUS, which carries no other value;

  • IDENT (identifier), which also carries a string value;

  • EOF, which carries no other value.

(We will see later, when discussing the lexer, that the values carried by the tokens LIT_INT and IDENT come from the Hygge0 source file we are compiling.)

Then, on lines 33–36, the sample of Parser.fsy above declares grammar rules for parsing an expression, which can be either:

  • an expression followed by the token PLUS and another expression; or

  • a value, which is a token LIT_INT (lines 39–40);

  • a variable, which is just an identifier (lines 43–44), which is just a token IDENT (lines 46–47).

(Notice the similarity between the grammar above and the one in Definition 1.)

The generated parser reads a stream of tokens — and whenever it matches one of the grammar rules above, it computes a result value by executing the code snippet next to the rule itself (between curly brackets). Our goal is to set up such code snippets in a way that recursively builds the UntypedAST of the input source code, based on how the grammar rules are matched.

In the sample of Parser.fsy above, the code snippets in lines 34–36 create AST nodes via the auxiliary function mkNode (here omitted), which inserts the position of the parsed expression. The code snippets use the values produced when parsing each symbol in their own rule, by referring to symbol position in the rule ($1, $2, …).

For instance, here is what happens when the parser is trying to parse an “expr”, according to its rules (lines 33–36).

  • Line 34. When “expr PLUS expr” matches, the parser creates an UntypedAST containing an expression Expr.Add($1, $3) — where $1 and $3 are the results produced when parsing the exprs on the left and right of PLUS (hence, both $1 and $3 are UntypedASTs).

  • Line 35. When “value” matches, the parser creates an AST node containing an expression Expr.IntVal($1), where $1 is the result produced when parsing the symbol value. To understand what is this result, we observe:

    • the rules for parsing value (lines 39–40) say that when value is parsed by matching a token LIT_INT, the result is $1, which is the value carried by the token itself.

  • Line 36. When “variable” matches, the parser creates an AST node containing an expression Expr.Var($1), where $1 is the result produced when parsing the symbol variable. To understand what is this result, we observe:

    • the rules for parsing variable (lines 43–44) say that when variable is parsed by matching a symbol ident, we just return $1, which is the value produced when parsing ident;

      • the rules for parsing ident (lines 46–47) say that they say that when ident is parsed by matching a token IDENT, the result is $1, which is the value carried by the token itself.

The Lexer Configuration File Lexer.fsl#

The tokens declared in the parser configuration file are recognised by the lexer — and the lexer configuration file Lexer.fsl specifies how this is done.

The file Lexer.fsl has the following structure: here we see a simplified fragment that only recognises a few tokens.

 1{
 2// Preamble with definitions of types and/or functions.  The code appearing here
 3// will be placed on top of the generated lexer source code.
 4}
 5
 6// Regular expressions used in the token rules below
 7let letter     = ['a'-'z'] | ['A'-'Z']
 8let digit      = ['0'-'9']
 9let litInt     = digit+
10let ident      = (letter | '_') (letter | '_' | digit)*
11// ...
12
13// We now define the rules for recognising the language tokens.  When a rule
14// matches, it produces a token, which is computed by running the snippet of F#
15// code next to the rule itself (between curly brackets).
16rule tokenize = parse
17// ...
18| litInt  { Parser.LIT_INT(...) }
19| "+"     { Parser.PLUS }
20| ident   { Parser.IDENT(...) }
21| eof     { Parser.EOF } // End of File

The configuration above contains, on lines 18–21, a series of rules: they specify what the lexer should do whenever it sees a sequence of input characters that matches a certain string or regular expression. When a rule matches, the lexer produces a token, which is computed by running the snippet of F# code next to the rule itself (between curly brackets).

For example:

  • line 16 says that if the input characters match the regular expression litInt (defined on line 9), then the lexer produces a token LIT_INT carrying the value matched by the regular expression (this part is omitted with “...”);

  • line 17 says that if a "+" character is seen, then the lexer produces a token PLUS.

Note

The actual configuration file Lexer.fsl used by hyggec contains more rules (here omitted) that discard “useless” groups of characters. For example:

  • whenever we see a white space or newline, we skip it, and continue lexing from the character that follows;

  • whenever we see "//" (the beginning of a comment) we skip all characters until we see and end-of-line, and continue lexing from the character that follows.

Example: the Lexer and Parser in Action#

We now have all ingredients to understand how the hyggec lexer and parser examine an input file, and turn it into a sequence of tokens, and then into an AST. This is detailed in Example 19 below.

Example 19 (Lexing and Parsing a Hygge0 Expression)

Let’s create a file called test.hyg, with the following content:

42 + x

When the hyggec lexer reads this file, it processes its contents character-by-character, grouping and classifying the characters according to the rules in The Lexer Configuration File Lexer.fsl. Therefore, the lexer sees the file contents as follows:

  • 42, that matches the rule on line 18. Consequently, the lexer produces a token LIT_INT carrying the value 42;

  • a white space, that is skipped;

  • +, that matches the rule on line 19. Consequently, the lexer produces a token PLUS;

  • a white space, that is skipped;

  • x, that matches the rule on line 20; Consequently, the lexer produces a token IDENT carrying the value "x";

  • the end of the file, which matches the rule on line 21. Consequently, the lexer produces a token EOF.

This sequence of tokens can be seen by executing:

./hyggec tokenize test.hyg

The output is:

[LIT_INT 42; PLUS; IDENT "x"; EOF]

This sequence of tokens is then processed by the parser, according to The Parser Configuration File Parser.fsy (Simplified). Therefore, the parser tries to parse the start symbol, called program (line 30); the only rule for program (line 31) requires to match an expr followed by an EOF token, and return the result $1 (produced by parsing expr). Consequently, the generated parser tries to match the sequence of tokens [LIT_INT 42; PLUS; IDENT "x"] against expr, and produce an UntypedAST as a result.

Fig. 4 provides a visual intuition of how the tokens [LIT_INT 42; PLUS; IDENT "x"] are matched against expr, and how the instance of UntypedAST shown in Example 18 is constructed:

  • the solid arrows (going up) show how the grammar rules in The Parser Configuration File Parser.fsy (Simplified) are applied (such rule applications describe the concrete syntax tree of the input file);

  • the dashed arrows (going down) show how the result of each rule is produced and propagated, building the abstract syntax tree instance shown in Example 18 (of type UntypedAST).

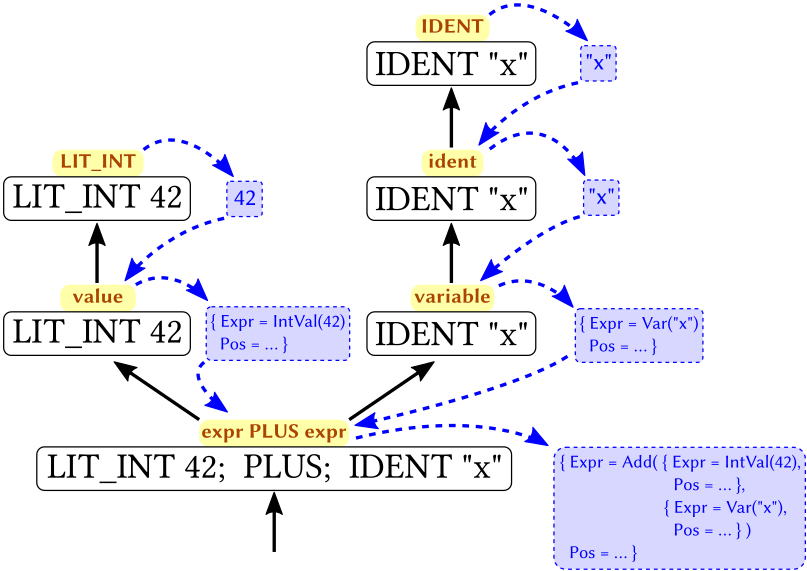
Depiction of how the parser processes a sequence of tokens

Fig. 4 How the parser generated from The Parser Configuration File Parser.fsy (Simplified) processes the sequence of tokens [LIT_INT 42; PLUS; IDENT "x"].#

More in detail, Fig. 4 depicts the following process:

  • among the rules for parsing expr (lines 34–36), the input tokens [LIT_INT 42; PLUS; IDENT "x"] are only compatible with the rule “expr PLUS expr” (line 34), which:

    1. recursively matches LIT_INT 42 as an expr via the rule on line 35, which:

      • recursively matches LIT_INT 42 as a value via the rule on line 40, which:

        • matches the token LIT_INT 42, and

        • produces 42

      • produces the AST node containing the expression IntVal(42);

    2. matches PLUS;

    3. recursively matches IDENT "x" as an expr via the rule on line 36, which:

      • recursively matches IDENT "x" as a variable via the rule on line 44, which:

        • recursively matches IDENT "x" as an ident via the rule on line 47, which:

          • matches token IDENT "x", and

          • produces "x"

        • produces "x";

      • produces the AST node containing the expression Var("x");

    4. finally, produces the AST node containing the expression Add($1, $3), where $1 and $3 are the AST nodes produced by matching the sub-expressions. Therefore:

      • $1 is replaced by the AST node containing IntVal(42), and

      • $3 is replaced by the AST node containing Var("x").

The corresponding AST produced by hyggec can be seen by running:

./hyggec parse test.hyg

The output is the following (where the AST nodes show their position of their expression in test.hyg, ranging from their initial to their final line:column coordinates).

Add (1:1-1:6)
┣╾lhs: IntVal 42 (1:1-1:2)
┗╾rhs: Var x (1:6-1:6)

The Real Parser.fsy#

To conclude this section about the hyggec lexer and parser, it is worth highlighting that The Parser Configuration File Parser.fsy (Simplified) shown above is very simplified. It conveys an intuition of how FsYacc works, but it has a crucial flaw: if implemented that way, Parser.fsy would describe an ambiguous grammar: see Example 20 below.

Example 20 (Ambiguity of the Simplified Parser.fsy)

Consider an input file woth the following content:

1 + 2 + 3

If we tokenize this file, we get the following sequence of tokens:

[LIT_INT 1; PLUS; LIT_INT 2; PLUS; LIT_INT 3; EOF]

If we pass such tokens to a parser generated from Parser.fsy as sketched in The Parser Configuration File Parser.fsy (Simplified), that parser could build two possible syntax trees.

One syntax tree is obtained by treating + as a left-associative operator, i.e. by interpreting the input as (1 + 2) + 3:

Add
┣╾lhs: Add
┃      ┣╾lhs: IntVal 1
┃      ┗╾rhs: IntVal 2
┗╾rhs: IntVal 3

The other syntax tree is obtained by treating + as a right-associative operator, i.e. by interpreting the input as 1 + (2 + 3):

Add
┣╾lhs: IntVal 1
┗╾rhs: Add
       ┣╾lhs: IntVal 2
       ┗╾rhs: IntVal 3

The parser generator FsYacc would signal the ambiguity described in Example 20 with obscure messages like:

shift/reduce error at state 47 on terminal XXXXX ...

For this reason, the real configuration file Parser.fsy breaks down the Hygge0 grammar into many rules, in order to enforce operator associativity and precedence, and remove any ambiguity. This follows the style of the Java grammar specification (but it is much simpler). For example, the rules for parsing additions and multiplications look as follows:

addExpr: // Additive expression
  | addExpr PLUS multExpr   { mkNode(..., Expr.Add($1, $3)) }
  | multExpr                { $1 }

multExpr: // Multiplicative expression
  | multExpr TIMES unaryExpr  { mkNode(..., Expr.Mult($1, $3)) }
  | unaryExpr                 { $1 }

unaryExpr: // ...

This makes addition left-associative, and forces the parser to only look for a multiplication after trying to parse an addition. The effect is that, when parsing e.g. 1 + 2 * 3 + 4, we get the expected AST:

Add
┣╾lhs: Add
┃      ┣╾lhs: IntVal 1
┃      ┗╾rhs: Mult
┃             ┣╾lhs: IntVal 2
┃             ┗╾rhs: IntVal 3
┗╾rhs: IntVal 4

References and Further Readings#

This tutorial by Thanos Papathanasiou gives a nice overview of FsLex and FsYacc. (Note: the implementation uses an old version of .NET, but it also works on newer versions if you tweak its .fsproj file.)

FsYacc generates a parser based on the LALR algorithm. To know more about this parsing algorithm (and others), and understand the limitations of FsYacc and the meaning of its error messages, you can have a look at:

  • Bill Campbell, Iyer Swami, Bahar Akbal-Delibas. Introduction to Compiler Construction in a Java World. Chapman and Hall/CRC, 2012. Available on DTU Findit.

    • Chapter 3.4 (Bottom-Up Deterministic Parsing)

The Built-In Interpreter#

hyggec includes an interpreter that can execute Hygge0 expressions (either typed or untyped). This interpreter is not necessary for developing a compiler: in fact, once hyggec has a typed AST (produced by Typechecker.fs), it can proceed directly to Code Generation. However, an interpreter can be useful in multiple ways:

  1. it provides a direct implementation of the Formal Semantics of Hygge0, to be used as a reference;

  2. it helps testing whether the compiler respects the Formal Semantics of Hygge0: an expression \(e\) compiled and executed under RARS must produce the same computations and outputs observed when interpreting \(e\);

  3. finally, the interpreter can be used inside the compiler for code optimisation (as we will see later in the course).

The Hygge0 interpreter is implemented in the file src/Interpreter.fs, following the Formal Semantics of Hygge0. Most of the interpreter’s types and functions take two type arguments 'E and 'T: they have the same meaning discussed in The AST Definition, and being generic, they allow the interpreter to support both typed and untyped ASTs.

The type RuntimeEnv defined in src/Interpreter.fs represents the runtime environment \(R\) in Structural Operational Semantics of Hygge0:

  type RuntimeEnv<'E,'T> = {
      Reader: Option<unit -> string>  // Used to read a console input
      Printer: Option<string -> unit> // Used to perform console output
  }

The function reduce is the core of src/Interpreter.fs, and it corresponds to the reduction formalised in Definition 4. The function takes a runtime environment and an AST node, and attempts to perform one reduction step:

  • if it succeeds, it returns Some with a pair consisting of a (possibly updated) runtime environment and reduced AST node;

  • if it cannot perform a reduction (because the AST node contains a value, or a stuck expression), it returns None.

let rec reduce (env: RuntimeEnv<'E,'T>)
               (node: Node<'E,'T>): Option<RuntimeEnv<'E,'T> * Node<'E,'T>> =
    match node.Expr with
    // ...

Each pattern matching case in the function reduce corresponds to a possible Hygge0 expression, and the function attempts to reduce the expression according to Definition 4. For example, values and variables cannot reduce (because there is no rule to let them reduce):

    | UnitVal
    | BoolVal(_)
    | IntVal(_)
    | FloatVal(_)
    | StringVal(_) -> None

    | Var(_) -> None

For an expression “\(\hygAssert{e}\)”, the function reduce follows rules \(\ruleFmt{R-Assert-Eval-Arg}\) and \(\ruleFmt{R-Assert-Res}\) in Definition 4:

  • if \(e\) is the boolean value \(\text{true}\), it proceeds by reducing the whole expression to the value unit (according to rule \(\ruleFmt{R-Assert-Res}\));

  • otherwise, it tries to recursively reduce \(e\):

    • if \(e\) reduces into \(e'\), then reduce returns an AST node with the updated expression \(e'\), by rule \(\ruleFmt{R-Assert-Eval-Arg}\) (notice that reduce creates the new AST node by copying and updating its original argument node);

    • if \(e\) cannot reduce, then \(e\) is stuck, and thus, reduce returns None (because the whole expression is stuck).

    | Assertion(arg) ->
        match arg.Expr with
        | BoolVal(true) -> Some(env, {node with Expr = UnitVal})
        | _ ->
            match (reduce env arg) with
            | Some(env', arg') -> Some(env', {node with Expr = Assertion(arg')})
            | None -> None

For an expression “\(\hygLetU{x}{e}{e_2}\)”, the function reduce follows rules \(\ruleFmt{R-Let-Eval-Init}\) and \(\ruleFmt{R-Let-Subst}\) in Definition 4. It tries to recursively reduce \(e\), and:

  • if \(e\) can reduce into \(e'\), it returns an AST node with the updated expression “\(\hygLet{x}{t}{e'}{e_2}\)” (by rule \(\ruleFmt{R-Let-Eval-Init}\));

  • if \(e\) cannot reduce bacause it is already a value \(v\), it substitutes \(x\) with \(v\) in \(e'\) (by rule \(\ruleFmt{R-Let-Subst}\)). In this case, reduce invokes ASTUtil.subst, which implements substitution according to Definition 2;

  • otherwise, \(e\) is stuck, and thus, reduce returns None (because the whole expression is stuck).

    | Let(name, init, scope) ->
        match (reduce env init) with
        | Some(env', init') ->
            Some(env', {node with Expr = Let(name, init', scope)})
        | None when (isValue init) ->
            Some(env, {node with Expr = (ASTUtil.subst scope name init).Expr})
        | None -> None

Exercise 19

Consider the following groups of reduction rules from Definition 4:

  • \(\ruleFmt{R-Sub-L}\), \(\ruleFmt{R-Sub-R}\), \(\ruleFmt{R-Sub-Res}\)

  • \(\ruleFmt{R-Mul-L}\), \(\ruleFmt{R-Mul-R}\), \(\ruleFmt{R-Mul-Res}\)

  • \(\ruleFmt{R-Seq-Eval}\), \(\ruleFmt{R-Seq-Res}\)

  • \(\ruleFmt{R-Type-Res}\)

  • \(\ruleFmt{R-Ascr-Res}\)

  • \(\ruleFmt{T-Print-Eval}\), \(\ruleFmt{T-Print-Res}\),

  • \(\ruleFmt{R-Read-Int}\), \(\ruleFmt{R-Read-Float}\)

For each group of reduction rules listed above:

  1. find the case of the function reduce (in the file src/Interpreter.fs) that implements reductions for the corresponding Hygge0 expression (e.g. in the case of \(\ruleFmt{T-Type-Res}\), find the case of reduce that handles the expression “\(\hygType{x}{t}{e}\)”);

  2. identify how the premises and conditions of the reduction rules are checked in reduce; and

  3. identify how the expression returned by reduce corresponds to the reduced expression in the conclusion of the reduction rules.

Exercise 20

Consider the reduction rules you wrote when solving Exercise 14. For each of those reduction rules:

  1. find the case of the function reduce (in the file src/Interpreter.fs) that implements reduction for the corresponding Hygge0 expression;

  2. identify how each premise and condition of your reduction rule is checked in reduce; and

  3. identify how the expression returned by reduce corresponds to the reduced expression in the conclusion of your reduction rule.

Do you see any discrepancy? If so, do you think there is a mistake in reduce, or in your reduction rule?

Tip

If you have not yet solved Exercise 14, you can proceed in the opposite direction: see how reduce handles a certain expression, and try to write down the corresponding reduction rule(s).

Types and Type Checking#

The hyggec type checker is implemented in the file src/Typechecker.fs, and its goal is to inspect an UntypedAST (produced by The Lexer and Parser), and either:

  • produce a TypedAST, where each AST node and expression has an associated type and typing environment (similarly to a typing derivation); or

  • report typing errors pointing at issues in the input source program.

Consequently, we represent the result of type checking as a type called TypingResult (defined in src/Typechecker.fs). The definition of TypingResult uses the standard Result type provided by F#, so a typing result is either Ok with a TypedAST, or Error with a list of type errors:

type TypingResult = Result<TypedAST, TypeErrors>

As mentioned in The AST Definition, the type TypedAST above is just an alias for type Node<TypingEnv, Type>, where:

  • the type Type (defined in the file src/Type.fs) is the internal representation of a Hygge0 type in the hyggec compiler, and follows Definition 5:

    type Type =
    | TBool                 // Boolean type.
    | TInt                  // Integer type.
    | TFloat                // Floating-point type (single-precision).
    | TString               // String type.
    | TUnit                 // Unit type.
    | TVar of name: string  // Type variable.

  • the type TypingEnv (defined in the file src/Typechecker.fs) is the internal representation of a Hygge0 typing environment in the hyggec compiler, and follows Definition 6:

    type TypingEnv = {
    Vars: Map<string, Type> // Variables in the current scope, with their type
    TypeVars: Map<string, Type> // Type vars in current scope, with their def.
}

Type Checking or Type Inference?#

Before proceeding, it is worth noticing that here (as in most literature about compilers) we often use the term “type checking” in a broad sense, meaning “analysing a source program to see whether it is well-typed”. But more precisely, to implement hyggec we need to solve a type inference problem, according to Definition 12 below.

Definition 12 (Type Checking vs. Type Inference)

Take a set of rules defining a typing judgement \(\hygTypeCheckJ{\Gamma}{e}{T}\) (such as the rules in Definition 8).

  • A type checking problem has the following form:

    • given a typing environment \(\Gamma\), an expression \(e\), and a type \(T\), construct a typing derivation that proves \(\hygTypeCheckJ{\Gamma}{e}{T}\)

  • A type inference problem has the following form:

    • given a typing environment \(\Gamma\) and an expression \(e\), find a type \(T\) for which we can construct a typing derivation that proves \(\hygTypeCheckJ{\Gamma}{e}{T}\)

Luckily, the Hygge0 typing rules in Definition 8 directly suggest us how to implement a type inference algorithm, because the rules are syntax-driven: just by looking at the shape of an expression \(e\), and reading the rules “bottom-up” (from the conclusion to the premises) we can determine which rule(s) could possibly be used to type \(e\), and what additional checks they require. For instance, suppose we are trying to infer the type of a Hygge0 expression \(e\):

  • if \(e\) is an integer value \(42\), we can only type it by rule \(\ruleFmt{T-Val-Int}\), hence we immediately infer that \(e\) has type \(\tInt\);

  • if \(e\) is a variable \(x\), we can only type it by rule \(\ruleFmt{T-Var}\), hence we infer that \(e\) must have the type contained in \(\envField{\Gamma}{Vars}(x)\). If \(x\) is not in \(\envField{\Gamma}{Vars}\), there is no other typing rule we can try, so we report a typing error;

  • if \(e\) is a logical negation “\(\hygNot{e'}\)”, then we can only type it by trying the typing rule you wrote as part of Exercise 17. Therefore, we recursively infer the type of \(e'\), and check whether \(e'\) has type \(\tBool\). If this is the case, we infer that \(e\) has type \(\tBool\); otherwise, there is no other typing rule we can try, so we report a typing error;

  • if \(e\) is an addition “\(e_1 + e_2\)”, then we can only type it by trying rule \(\ruleFmt{T-Add}\). Therefore, we recursively infer the types of \(e_1\) and \(e_2\), and check whether:

    • both \(e_1\) and \(e_2\) have type \(\tInt\) — and in this case, we infer that \(e\) has type \(\tInt\); or

    • both \(e_1\) and \(e_2\) have type \(\tFloat\) — and in this case, we infer that \(e\) has type \(\tFloat\).

    If this doesn’t work, there is no other typing rule we can try, so we report a typing error;

  • if \(e\) is a conditional “\(\hygCond{e_1}{e_2}{e_3}\)”, we can only type it by trying rule \(\ruleFmt{T-Cond}\). Therefore, we recursively infer the types of \(e_1\), \(e_2\), and \(e_3\), and check whether:

    • \(e_1\) has type \(\tBool\), and

    • \(e_1\) and \(e_2\) have a same type \(T\) — and in this case, we infer that \(e\) has that type \(T\).

    If this doesn’t work, there is no other typing rule we can try, so we report a typing error.

Implementation of src/Typechecker.fs#

The core of src/Typechecker.fs is a function called typer, which implements the type inference algorithm discussed above. The function typer has the following definition: it takes a typing environment and an AST node, performs a pattern matching against the expression contained in the AST node, and returns a TypingResult.

let rec typer (env: TypingEnv) (node: UntypedAST): TypingResult =
    match node.Expr with
    // ...

The function typer is initially called with an empty environment, and with the whole AST of the Hygge0 program being compiled. While running, typer recursively traverses the AST, adding information to the environment, as required by the typing rules in Definition 8.

Each case in typer takes the given AST node (which is untyped), and (if type inference succeeds) produces a typed AST node containing the current environment, and the inferred type. Otherwise, typer returns a list of typing errors.

For example, typer assigns types to boolean or integer values, as follows:

    | BoolVal(v) ->
        Ok { Pos = node.Pos; Env = env; Type = TBool; Expr = BoolVal(v) }
    | IntVal(v) ->
        Ok { Pos = node.Pos; Env = env; Type = TInt; Expr = IntVal(v) }

When typing a variable, typer checks whether the variable is in the typing environment, and assigns the type it finds there to the variable — or reports an error:

    | Var(name) ->
        match (env.Vars.TryFind name) with
        | Some(tpe) ->
            Ok { Pos = node.Pos; Env = env; Type = tpe; Expr = Var(name) }
        | None ->
            Error([(node.Pos, $"undefined variable: %s{name}")])

When typing a logical “not” expression, typer recursively infers the type of the argument, and checks whether it is a subtype of \(\tBool\): if so, typer infers that the whole expression has type \(\tBool\); otherwise, it reports type errors.

    | Not(arg) ->
        match (typer env arg) with
        | Ok(targ) when (isSubtypeOf env targ.Type TBool) ->
            Ok { Pos = node.Pos; Env = env; Type = TBool; Expr = Not(targ) }
        | Ok(arg) ->
            Error([(node.Pos, $"expected %O{TBool} arg, found %O{arg.Type}")])
        | Error(es) -> Error(es)

Important

In the last example above (3rd line) we are using isSubtypeOf (defined in src/Typechecker.fs) to compare the types targ.Type and TBool. This check corresponds to an application of the subsumption rule in Definition 11: we want targ to have type \(\tBool\), so it is OK if targ has a subtype of \(\tBool\) (e.g. via some type alias).

Instead of using isSubtypeOf, in the code above we could have simply written targ.Type = TBool: this would work, but it would also make our typing system less flexible, leading to limitations similar to those discussed in Example 16.

Therefore, the rule of thumb is: whenever typer needs to compare two types, it should use isSubtypeOf (instead of plain equality =).

One may ask: instead of checking subtyping in multiple places, can we implement a general type inference case based on the subsumption rule \(\ruleFmt{T-Sub}\) in Definition 11?

The answer, unfortunately, is no — and the reason is that (unlike the typing rules in Definition 8) rule \(\ruleFmt{T-Sub}\) is not syntax-driven: it can be applied to any expression \(e\). Therefore, we need to explicitly check subtyping whenever we compare types.

The rest of the pattern matching cases inspected by the function typer work similarly. Two things to mention:

  • in the cases for “\(\hygLet{x}{t}{e_1}{e_2}\)” and “\(\hygType{x}{t}{e}\)”, typer need to check whether the pretype \(t\) corresponds to some valid type \(T\). To this end, typer uses the function resolvePretype, which corresponds to the type resolution judgement in Definition 7;

  • in various cases, typer uses auxiliary functions to avoid code duplication. For instance: “\(e_1 + e_2\)” and “\(e_1 * e_2\)” are typed in a similar way (see rule \(\ruleFmt{T-Add}\) in Definition 8, and Exercise 17), and thus, typer uses a function called binaryNumericalOpTyper to handle both.

Example 21 (Untyped vs. Typed ASTs)

To see the difference between the untyped AST and the typed AST of a Hygge0 program, you can try to parse the example in Example 3:

./hyggec parse examples/hygge0-spec-example.hyg

And then compare the untyped AST above with the typed AST produced by src/Typechecker.fs:

./hyggec typecheck examples/hygge0-spec-example.hyg

Exercise 21

Consider the following typing rules from Definition 8:

  • \(\ruleFmt{T-Seq}\)

  • \(\ruleFmt{T-Assert}\)

  • \(\ruleFmt{T-Ascr}\)

  • \(\ruleFmt{T-Print}\)

  • \(\ruleFmt{T-Let}\)

  • \(\ruleFmt{T-Type}\)

For each typing rule listed above:

  1. find the case of the function typer (in the file src/Typechecker.fs) that implements type inference for the corresponding Hygge0 expression (e.g. in the case of \(\ruleFmt{T-Seq}\), find the case of typer that handles the expression \(e_1; e_2\));

  2. identify how each premise of the typing rule is checked in typer; and

  3. identify how the type inferred by typer matches the type expected in the conclusion of the typing rule.

Exercise 22

Consider the typing rules you wrote when solving Exercise 17. For each one of those typing rules:

  1. find the case of the function typer (in the file src/Typechecker.fs) that implements type inference for the corresponding Hygge0 expression;

  2. identify how each premise of your typing rule is checked in typer; and

  3. identify how the type inferred by typer matches the type expected in the conclusion of your typing rule.

Do you see any discrepancy? If so, do you think there is a mistake in typer, or in your typing rule?

Tip

If you have not yet solved Exercise 17, you can proceed in the opposite direction: see how typer handles a certain expression, and try to write down a corresponding typing rule.

Code Generation#

The code generation of hyggec is implemented in the file src/RISCVCodegen.fs. We illustrate its contents when discussing the Code Generation Strategy — but first, we have a look at the RISC-V Code Generation Utilities.

RISC-V Code Generation Utilities#

The file src/RISCV.fs contains various data types and functions to represent RISC-V assembly code, and manipulate assembly code snippets. The hyggec compiler goal is to produce text output containing RISC-V assembly — and this internal representation of the output code makes the job simpler, and prevents possible mistakes.

The key components of src/RISCV.fs are the following (we will see them in use in the Code Generation Strategy).

  • The type RV (standing for “RISC-V”) represents a statement in a RISC-V assembly program: it is a discriminated union with one named case for each supported RISC-V instruction (e.g. the RISC-V instruction mv is represented by the named case RV.MV(...)). It also includes named cases for representing labels and comments in RISC-V assembly.

  • The types Reg and FPReg represent, respectively, a base integer register and a floating-point register. Their purpose is twofold:

    1. they help ensuring that the RISC-V instructions in RV above can only be used with registers that exist, and have the correct type (otherwise, the F# compiler reports a type error). For example:

      • we cannot use the instruction RV.MV(...) on a floating-point register — if we try, we get an F# type error;

      • to move a value from register t0 to t1, we can write RV.MV(Reg.t1, Reg.t0) — and if there is a typo (e.g. if we write “RV.MV(Reg.t1, Reg.y0)”) it will be spotted by the F# compiler;

    2. they provide generic numbered registers Reg.r(n) and FPReg.r(n), which range over all “temporary” and “saved” RISC-V registers. For example, to move a value from generic register number \(n+1\) to \(n\), one can write: RV.MV(Reg.r(n), Reg.r(n+1)). This greatly simplifies the handling of registers during code generation.

  • The type Asm represents an assembly program with its .data and .text segments. The main features are:

    • the methods addData and addText, which allow us to add memory allocations and instructions in the selected memory segment; and

    • the method ++, which allows us to combine two assembly programs (e.g. produced during code generation) into a unique, well-formed assembly program.

Code Generation Strategy#

The core of the file src/RISCVCodegen.fs is the function doCodegen, which takes a code generation environment and a typed AST node, and produces assembly code. Correspondingly, the declaration of doCodegen has the following types.

let rec doCodegen (env: CodegenEnv) (node: TypedAST): Asm = // ...

The function doCodegen uses a very simple code generation strategy. In a nutshell, when compiling an expression \(e\):

  • after \(e\) is computed, its result is written in a target register with number \(n\);

  • if the computation of \(e\) requires the results of other sub-expressions, then doCodegen recursively compiles each sub-expression by increasing (if necessary) their target register numbers to \(n+1\), \(n+2\), etc.

Important

This compilation strategy only works if the code produced by each doCodegen recursive call never modifies any register with a number lower than the current target.

With this approach, the code generation environment (of type CodegenEnv) used by doCodegen must contain two pieces of information:

  1. which target register number should be used to compile the current expression. More precisely, we need one target for integer expressions, and another target for floating-point expressions; and

  2. a “storage” mapping from known variable names, to the location where the value of each variable is stored (e.g. in a register, or in memory).

Consequently, the CodegenEnv type is a record that looks as follows:

type CodegenEnv = {
    Target: uint      // Target register for the result of integer expressions
    FPTarget: uint      // Target register for the result of float expressions
    VarStorage: Map<string, Storage>     // Storage info about known variables
}

The type Storage used by CodegenEnv tells us whether the value of a variable is stored in an integer register, or in a floating-point register, or in a memory location marked with a label in the generated assembly code.

type Storage =
    | Reg of reg: Reg     // The value is stored in an integer register
    | FPReg of fpreg: FPReg  // The value is stored in a float register
    | Label of label: string // Value is stored in memory, with a label

A Tour of doCodegen#

We now have all ingredients to examine how doCodegen works. Its implementation is a pattern matching on the expression contained in the AST node being compiled.

let rec doCodegen (env: CodegenEnv) (node: TypedAST): Asm =
    match node.Expr with
    // ...

Here are some examples of how doCodegen’s main pattern matching handles various kinds of expressions.

An integer value is immediately loaded into the target register (using the assembly instruction li).

    | IntVal(v) ->
        Asm(RV.LI(Reg.r(env.Target), v))

Example 22 (Compiling an Integer)

If we compile the Hygge0 expression 42, the match case for IntVal above is executed, and the output of the compiler is:

.data:

.text:
    li t0, 42            # <-- Produced by match case for IntVal in doCodegen
    li a7, 10  # RARS syscall: Exit
    ecall  # Successful exit with code 0

A string value is added to the .data segment of the generated assembly code, with its memory address marked by a unique label (generated with the function Util.genSymbol). Then, the memory address is loaded into the target register (using the assembly instructions la).

    | StringVal(v) ->
        let label = Util.genSymbol "string_val"
        Asm().AddData(label, Alloc.String(v))
             .AddText(RV.LA(Reg.r(env.Target), label))

Example 23 (Compiling a String)

If we compile the Hygge0 expression "Hello, World!", the match case for StringVal above is executed, and the output of the compiler is:

.data:
string_val:
    .string "Hello, World!"  # <-- Produced by case for StringVal in doCodegen

.text:
    la t0, string_val  # <-- Produced by match case for StringVal in doCodegen
    li a7, 10  # RARS syscall: Exit
    ecall  # Successful exit with code 0

When compiling an addition “\(e_1 + e_2\)” with target register \(n\), doCodegen proceeds as follows:

  1. recursively generates the assembly code for \(e_1\), targeting the register \(n\);

  2. recursively generates the assembly code for \(e_2\), targeting the register \(n+1\);

  3. generates a RISC-V addition operation that adds the contents of registers \(n\) and \(n+1\), and overwrites register \(n\) with the result.

The resulting code looks, intuitively, as follows.

    | Add(lhs, rhs)
        let lAsm = doCodegen env lhs    // Generated code for the lhs expression
        
        match node.Type with   // Generated code depends on the type of addition
        | t when (isSubtypeOf node.Env t TInt) ->
            let rtarget = env.Target + 1u  // Target register for rhs expression
            let rAsm = doCodegen {env with Target = rtarget} rhs  // Asm for rhs
            let opAsm =             // Generated code for the addition operation
                Asm(RV.ADD(Reg.r(env.Target),
                           Reg.r(env.Target), Reg.r(rtarget)))
            lAsm ++ rAsm ++ opAsm  // Put asm code together: lhs, rhs, operation

        | t when (isSubtypeOf node.Env t TFloat) ->
            // ** Omitted code similar to above, with float regs and instructs

        | t ->
            failwith $"BUG: addition codegen invoked on invalid type %O{t}"

Note

In the actual hyggec implementation is a bit different: since addition “\(e_1 + e_2\)” and multiplication “\(e_1 * e_2\)” generate very similar code, the pattern matching case above handles both Add(lhs, rhs) and Mult(lhs, rhs) — and in case of multiplication, it produces the RISC-V instruction mul (instead of add).

When compiling a variable \(x\), doCodegen produces code to access the value of the variable, depending on where it is stored: to this end, it inspects the VarStorage mapping in the code generation environment. (For clarity of exposition, the code snippet below omits some cases that are present in the implementation).

    | Var(name) ->
        match node.Type with   // Inspect the var type and where it is stored
        | t when (isSubtypeOf node.Env t TFloat) ->
            match (env.VarStorage.TryFind name) with
            | Some(Storage.FPReg(fpreg)) ->
                Asm(RV.FMV_S(FPReg.r(env.FPTarget), fpreg),
                    $"Load variable '%s{name}'")
            | _ -> failwith $"BUG: float var with bad storage: %s{name}"

        | _ ->      // Default case for variables holding integer-like values
            match (env.VarStorage.TryFind name) with
            | Some(Storage.Reg(reg)) ->
                Asm(RV.MV(Reg.r(env.Target), reg), $"Load variable '%s{name}'")
            | _ -> failwith $"BUG: variable without storage: %s{name}"

When compiling a “let” expression “\(\hygLetU{x}{e_1}{e_2}\)” or “\(\hygLet{x}{t}{e_1}{e_2}\)” with target register \(n\), doCodegen proceeds as follows:

  • recursively generates assembly code for \(e_1\), targeting the register \(n\);

  • adds the variable \(x\) to the env.VarStorage mapping, assigning it to register \(n\) (which contains the result of \(e_1\));

  • compiles \(e_2\) with the updated env.VarStorage (containing \(x\)), targeting register \(n+1\) (because \(e_2\) may use \(x\), and thus its code may use the register \(n\));

  • copies the result of \(e_2\) from register \(n+1\) to \(n\) (thus overwriting the value of \(x\), which is going out of scope).

    | Let(name, init, scope) 
    | LetT(name, _, init, scope) ->
        let initCode = doCodegen env init  // 'let...' initialisation asm code
        match init.Type with
        | t when (isSubtypeOf init.Env t TFloat) ->
            // ** Omitted code similar to the following, using float registers

        | _ ->     // Default case for integer-like initialisation expressions
            let scopeTarget = env.Target + 1u   // Target reg. for 'let' scope
            let scopeVarStorage =     // Var storage for compiling 'let' scope
                env.VarStorage.Add(name, Storage.Reg(Reg.r(env.Target)))
            let scopeEnv = { env with Target = scopeTarget
                                      VarStorage = scopeVarStorage }
            initCode
                ++ (doCodegen scopeEnv scope)
                    .AddText(RV.MV(Reg.r(env.Target), Reg.r(scopeTarget)),
                             "Move 'let' scope result to target register")

Example 24 (Compiling a “Let…” and an Addition)

Consider the following Hygge0 program:

let x = 42;
x + 3

If we save this program in a file example.hyg, we can see its typed AST by executing:

./hyggec typecheck example.hyg

The typed AST looks as follows: (we omit Env.TypeVars for brevity)

Let x (1:1-2:5)
┣╾Env.Vars: ∅
┣╾Type: int
┣╾init: IntVal 42 (1:9-1:10)
┃       ┣╾Env.Vars: ∅
┃       ┗╾Type: int
┗╾scope: Add (2:1-2:5)
         ┣╾Env.Vars: Map
         ┃           ┗╾x: int
         ┣╾Type: int
         ┣╾lhs: Var x (2:1-2:1)
         ┃      ┣╾Env.Vars: Map
         ┃      ┃           ┗╾x: int
         ┃      ┗╾Type: int
         ┗╾rhs: IntVal 3 (2:5-2:5)
                ┣╾Env.Vars: Map
                ┃           ┗╾x: int
                ┗╾Type: int

To compile the program above, we can execute:

./hyggec compile example.hyg

Then, hyggec produces the following RISC-V assembly code.

.data:

.text:
    li t0, 42                   # <-- Produced by case for IntVal in doCodegen
    mv t1, t0  # Load variable 'x' # <-- Produced by case for Var in doCodegen
    li t2, 3                    # <-- Produced by case for IntVal in doCodegen
    add t1, t1, t2                 # <-- Produced by case for Add in doCodegen
    mv t0, t1  # Move 'let' scope result to 'let' target register
    li a7, 10  # RARS syscall: Exit
    ecall  # Successful exit with code 0

Note

The function doCodegen includes more cases, which follow the explanations above. The only exceptions are those that require RARS system calls (e.g. Print, ReadInt: their code generation makes use of functions that save register values on the stack, and restore registers values from the stack. We will address these aspects later in the course.

Important

The Code Generation Strategy illustrated in this module is quite simple, and it has an important flaw: its naive register allocation policy tends to increase the target register number for each sub-expression being compiled — and in some cases, it may run out of available registers. When this happens, the hyggec compiler crashes, reporting a “BUG”.

Luckily, it takes some effort to write a Hygge0 program that triggers this limitation: therefore, it is unlikely that, by chance, you will write a program that stumbles into the issue. (See Exercise 23 below.)

We will consider better register allocation strategies later in the course.

Exercise 23 (Running Out of Registers)

Write a Hygge0 expression that, by the Code Generation Strategy, causes doCodegen to run out of registers, and makes hyggec crash.

Hint

There is a solution that only uses +, some integer values, and parentheses…

The Test Suite of hyggec#

We conclude this overview by mentioning the hyggec test suite, which is designed to encourage frequent testing of the compiler. To launch the test suite, simply invoke:

./hyggec test

Or, equivalently:

dotnet test

When running, the testing framework explores the tree of directories under tests/, and uses each file with extension .hyg as a test case. The outcome of the test depends on the position of the .hyg file in the tests/ directory tree, according to the following table. (Note that the .hyg files under the fail/ directories are expect to cause some error, in specific ways.)

Table 5 Overview of the hyggec directory tree for tests.#

Directory under tests/

A .hyg file under this directory is a passed test if…

lexer/pass/

The tokenization succeeds.

lexer/fail/

The tokenization fails with a lexer error.

parser/pass/

Parsing succeeds.

parser/fail/

Tokenization succeeds, but parsing fails.

interpreter/pass/

Tokenization and parsing succeed, and the interpreter reduces the program into a value.

interpreter/fail/

Tokenization and parsing succeed, but the interpreter reaches a stuck expression (e.g. assert(false)).

typechecker/pass/

Tokenization, parsing, and type checking succeed.

typechecker/fail/

Tokenization and parsing succeed, but type checking fails.

codegen/pass/

Tokenization, parsing, and type checking succeed, and the generated RISC-V assembly program runs under RARS and terminates successfully (exit code 0).

codegen/fail/

Tokenization, parsing, and type checking succeed, and the generated RISC-V assembly program runs under RARS, but it terminates with an assertion violation (assert(false)).

Example: Extending Hygge0 and hyggec with a Subtraction Operator#

The following sections show how to extend the Hygge0 language and the hyggec compiler with a subtraction operator, in 8 steps:

  1. Defining the Formal Specification of Subtraction

  2. Extending the AST

  3. Extending the Pretty Printer

  4. Extending the Lexer

  5. Extending the Parser

  6. Extending the Interpreter

  7. Extending the Type Checker

  8. Extending the Code Generation

To perform these steps, we use as a reference the most similar expression that is already supported by Hygge0 and hyggec — i.e. the addition \(e_1 + e_2\).

Formal Specification of Subtraction#

Before jumping to the implementation, we specify the formal syntax, semantics, and typing rules of the new subtraction operator.

First, we specify the syntax of subtraction expressions by extending the grammar rules of Hygge0 in Definition 1. We add a new rule:

\[\begin{split} \begin{array}{rrcll} \text{Expression} & e & ::= & \ldots \\ & & \mid & e_1 - e_2 & \text{(Subtraction)} \end{array} \end{split}\]

Then, we specify the semantics of subtraction expressions, in two steps.

  1. We specify how to substitute variable \(x\) with expression \(e'\) inside a subtraction \(e_1 - e_2\), by extending Definition 2 with a new case (similar to the existing case for addition):

    \[ \subst{(e_1 - e_2)}{x}{e'} \;\;=\;\; \subst{e_1}{x}{e'} - \subst{e_2}{x}{e'} \]

  2. We extend the reduction rules in Definition 4 with new rules for subtraction expressions (very similar to the existing rules for addition):

    \[\begin{split} \begin{array}{c} \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-Sub-L}{$\hygEvalConf{R}{e - e_2} \;\to\; \hygEvalConf{R'}{e' - e_2}$} \end{prooftree} \quad \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-Sub-R}{$\hygEvalConf{R}{v - e} \;\to\; \hygEvalConf{R'}{v - e'}$} \end{prooftree} \\ \begin{prooftree} \AxiomC{$v_1 - v_2 = v_3$} \UnaryInfCLab{R-Sub-Res}{$\hygEvalConf{R}{v_1 - v_2} \;\to\; \hygEvalConf{R}{v_3}$} \end{prooftree} \end{array} \end{split}\]

Finally, we extend the typing rules in Definition 8 with a new rule for subtraction expressions (very similar to the existing typing rule for addition):

\[ \begin{prooftree} \AxiomC{$T \in \{\text{int}, \text{float}\}$} \AxiomC{$\Gamma \vdash e_1 : T$} \AxiomC{$\Gamma \vdash e_2 : T$} \TrinaryInfCLab{T-Subtract}{$\Gamma \vdash e_1 - e_2 : T$} \end{prooftree} \]

Extending the AST#

We can now implement the Formal Specification of Subtraction. The first step is to extend the AST, by extending the type Expr<'E,'T> (in the file src/AST.fs) with a new case:

and Expr<'E,'T> = // ...
    /// Subtraction between lhs and rhs.
    | Sub of lhs: Node<'E,'T>
           * rhs: Node<'E,'T>

Tip

By extending the type Expr<'E,'T>, we will cause various warning in several source files, with messages like:

Incomplete pattern matches on this expression. For example, the value 'Sub (_, _)' may indicate a case not covered by the pattern(s)

These warnings highlight the parts of the hyggec source code we need to adjust to support the new AST case we have just added.

To see all such warnings on the console, we can rebuild hyggec by running:

dotnet clean

followed by

dotnet build

Extending the Pretty Printer#

hyggec needs to know how to display the new subtraction expression when printing an AST on screen. To this purpose, we add a new pattern matching case to the function formatASTRec (in the file src/PrettyPrinter.fs) to support the new case Sub(lhs, rhs) (we can copy and adapt the existing case for Add(lhs, rhs)):

    | Sub(lhs, rhs) ->
        mkTree "Sub" node [("lhs", formatASTRec lhs)
                           ("rhs", formatASTRec rhs)]

We will see the effect of this change shortly, when Testing the Parser.

Extending the Lexer#

We can now add a new rule to the lexer, to recognise the new token for the subtraction symbol “-”. In the file src/Lexer.fsl, we add the following line (e.g. nearby the definition for the token for “+”):

| "+"          { Parser.PLUS }
| "-"          { Parser.MINUS }  // <-- We add this line

Correspondingly, we must add declaration of Parser.MINUS in the file src/Parser.fsy. For instance, we can add MINUS nearby the other arithmetic operators:

// Tokens for arithmetic operators
%token TIMES PLUS MINUS    // <-- We add "MINUS" here

Testing the Lexer#

To see whether the lexer recognises the new token, we can add a new test. For example, we can add a file called tests/lexer/pass/003-minus.hyg containing just a minus sign:

-

And now, if we run

./hyggec tokenize tests/lexer/pass/003-minus.hyg

we should see (besides the warnings about incomplete pattern matches):

[MINUS; EOF]

Moreover, running hyggec test should not report any failed test.

Extending the Parser#

We can now add a new grammar rule for subtraction to the file src/Parser.fsy. Since subtraction should have the same operator precedence of addition, we can look for the rule for addition, and place the new rule in the same group of “additive expressions”:

// Additive expression
addExpr:
  | addExpr PLUS multExpr   { mkNode(parseState, 2, Expr.Add($1, $3)) }
  | addExpr MINUS multExpr  { mkNode(parseState, 2, Expr.Sub($1, $3)) }
  | multExpr                { $1 }

Important

Each time we modify the grammar rules of src/Parser.fsy, we should check whether we have introduced any parsing issue. To this purpose, we should run:

dotnet build

The messages produced by FsYacc should look like:

  computing first function...        time: 00:00:00.0571261
  building kernels...        time: 00:00:00.0253194
  building kernel table...        time: 00:00:00.0077130
  computing lookahead relations.................................................................................................        time: 00:00:00.0250216
  building lookahead table...        time: 00:00:00.0066406
  building action table...        time: 00:00:00.0114085
          building goto table...        time: 00:00:00.0022120
          returning tables.
  writing tables to log
          building tables
          94 states
          19 nonterminals
          36 terminals
          47 productions
          #rows in action table: 94

The output above has no errors, and this means that src/Parser.fsy is correct.

Instead, if we see an error message like the following, then our change to src/Parser.fsy has introduced a problem (probably a grammar ambiguity) and we should revise our change.

shift/reduce error at state 47 on terminal PLUS between...

Testing the Parser#

To see whether the parser recognises subtraction expressions, we can add a new test. For example, we can add a file called tests/parser/pass/011-minus.hyg containing:

42 - x

And now, if we run

./hyggec parse tests/parser/pass/011-minus.hyg

we should see (besides the warnings about incomplete pattern matches) a representation of the AST node for Sub (with the formatting we added by Extending the Pretty Printer):

Sub (1:1-1:6)
┣╾lhs: IntVal 42 (1:1-1:2)
┗╾rhs: Var x (1:6-1:6)

If the type of the subtraction does not match the type ascription, hyggec reports a typing error. After we add this test, running ./hyggec test should not report any failed test.

Extending the Interpreter#

In the Formal Specification of Subtraction, we have defined new reduction rules that are quite similar to those for addition. Correspondingly, we can extend the hyggec interpreter by adapting existing cases for addition, in two steps:

  1. we extend the function subst in src/ASTUtil.fs by adding a new case for Sub(lhs, rhs) (adapted from the existing case for Add(lhs, rhs)):

        | Sub(lhs, rhs) ->
        {node with Expr = Sub((subst lhs var sub), (subst rhs var sub))}

  2. we extend the function reduce in src/Interpreter.fs by adding a new case for Sub(lhs, rhs) (adapted from the existing case for Add(lhs, rhs)):

        | Sub(lhs, rhs) ->
        match (lhs.Expr, rhs.Expr) with
        | (IntVal(v1), IntVal(v2)) -> Some(env, {node with Expr = IntVal(v1 - v2)})
        | (FloatVal(v1), FloatVal(v2)) -> Some(env, {node with Expr = FloatVal(v1 - v2)})
        | (_, _) ->
            match (reduceLhsRhs env lhs rhs) with
            | Some(env', lhs', rhs') -> Some(env', {node with Expr = Sub(lhs', rhs')})
            | None -> None

Testing the Interpreter#

To test whether the interpreter handles subtraction expressions correctly, we can check whether the result of a subtraction is the value we expect. We can obtain this by writing a test case called e.g. tests/interpreter/pass/008-sub.hyg, with the following content:

assert(42 - 10 = 32);
assert(3.14f - 1.0f = 2.14f)  // Careful when comparing floats! This case is OK

If the any of the comparisons inside the assertions is false, the interpreter reaches a stuck expression \(\hygAssert{\hygFalse}\) and reports an error. After we add this test, running ./hyggec test should not report any failed test.

Extending the Type Checker#

In the Formal Specification of Subtraction, we have defined new typing rule \(\ruleFmt{T-Subtract}\) that is quite similar to rule \(\ruleFmt{T-Add}\) in Definition 8. Correspondingly, we can extend the hyggec function typer (in the file src/Typechecker.fs) with a new pattern matching case, based on the existing case for Add(lhs, rhs):

    | Sub(lhs, rhs) ->
        match (binaryNumericalOpTyper "subtraction" node.Pos env lhs rhs) with
        | Ok(tpe, tlhs, trhs) ->
            Ok { Pos = node.Pos; Env = env; Type = tpe; Expr = Sub(tlhs, trhs) }
        | Error(es) -> Error(es)

Testing the Type Checker#

To test whether the type checking for subtraction expressions works as intended, we can check whether the subtraction of two integers has type \(\tInt\), and whether the subtraction of two floating-point values has type \(\tFloat\). We can obtain this by writing a test case called e.g. tests/typechecker/pass/011-sub.hyg, with the following content:

(2 - 1): int;
(3.14f - 1.0f): float

Extending the Code Generation#

Code generation for subtraction is very similar to addition (and also multiplication): the only difference is that we need to emit the RISC-V assembly instruction sub (for integers) or fsub.s (for floating point values). Consequently, it is enough to edit the function doCodegen (in the file src/RISCVCodegen.fs) and find the pattern matching case for Add(lhs, rhs) (and also Mul(lhs, rhs)) and apply the following three changes:

  1. we extend the pattern matching case to also cover Sub(lhs, rhs):

        | Add(lhs, rhs)
    | Sub(lhs, rhs)  // <-- We add this line
    | Mult(lhs, rhs) as expr ->

  2. we find the internal pattern matching that generates the assembly instruction for a numerical operation on integer values. We extend that pattern matching with a new case for Sub(_,_):

                 match expr with
                 | Add(_,_) ->
                     Asm(RV.ADD(Reg.r(env.Target),
                                Reg.r(env.Target), Reg.r(rtarget)))
                 | Sub(_,_) ->                      // <-- We add this case
                     Asm(RV.SUB(Reg.r(env.Target),
                                Reg.r(env.Target), Reg.r(rtarget)))
                 | Mult(_,_) ->
                     Asm(RV.MUL(Reg.r(env.Target),
                                Reg.r(env.Target), Reg.r(rtarget)))

  3. finally, we find the internal pattern matching that generates the assembly instruction for a numerical operation on float values. We extend that pattern matching with a new case for Sub(_,_):

                match expr with
            | Add(_,_) ->
                Asm(RV.FADD_S(FPReg.r(env.FPTarget),
                              FPReg.r(env.FPTarget), FPReg.r(rfptarget)))
            | Sub(_,_) ->                         // < -- We add this case
                Asm(RV.FSUB_S(FPReg.r(env.FPTarget),
                              FPReg.r(env.FPTarget), FPReg.r(rfptarget)))
            | Mult(_,_) ->
                Asm(RV.FMUL_S(FPReg.r(env.FPTarget),
                              FPReg.r(env.FPTarget), FPReg.r(rfptarget)))

Testing the Code Generation#

To test the code generation, we can often reuse the same test cases of the interpreter, with assertions that stop the program execution if the result of a computation is not what we expect.

Consequently, we can create test case called e.g. tests/codegen/pass/008-sub.hyg with the same content used for Testing the Interpreter. After we add this test, running ./hyggec test should not report any failed test.

Note

When we reach this point, we should have fixed all the warnings caused by the addition of case Sub(lhs, rhs) in src/AST.fs. To double-check, we can rebuild hyggec by executing dotnet clean and then dotnet build. The result should be:

Build succeeded.
    0 Warning(s)
    0 Error(s)

Project Ideas#

For your group project, you should implement all the following (easy) project ideas (but notice that some of them give you a choice between different options). These project ideas will allow you to become familiar with the hyggec compiler internals.

You also have the option of choosing the following medium- or hard-difficulty project ideas, instead of (or in addition to) the above (but it is better to start with easy ideas for gaining experience):

Note

These project ideas are tailored for whole project groups. If you have not yet joined a group, you can address part of them (e.g. implement only one new arithmetic operator instead of 3), and later combine your work with your teammates.

Project Idea (Easy): Extend Hygge0 and hyggec with New Arithmetic Operations#

Add some new arithmetic operations to the Hygge0 language and to the hyggec compiler, by following the steps described in Example: Extending Hygge0 and hyggec with a Subtraction Operator. Choose at least 3 operations between:

  • Division “\(e_1 / e_2\)” (both integer and floating point)

  • Remainder “\(e_1 \mathbin{\%} e_2\)” (only between integers)

  • Square root “\(\text{sqrt}(e)\)” (only floating point)

    Hint

    To perform lexing and parsing of the new \(\text{sqrt}\) operation, you will need to:

    • define a new token matching “\(\text{sqrt}\)”; you may call this token e.g. SQRT. Then,

    • in src/Parser.fsy, add a new rule to parse an occurrence of SQRT, followed by LPAR (left parenthesis), followed by an expression, followed by RPAR (right parenthesis). You can use as a reference the existing rule that parses e.g. a print expression: it is located under unaryExpr and it looks like the following.

      // Unary expression
unaryExpr:
  // ... some rules omitted ...
  | PRINT LPAR simpleExpr RPAR    { mkNode(parseState, 1, Expr.Print($3)) }

      The new “\(\text{sqrt}(e)\)” expression should have the same precedence of “\(\hygPrint{e}\)”, so it should also be placed under unaryExpr.

  • Maximum “\(\text{max}(e_1, e_2)\)” and minimum “\(\text{min}(e_1, e_2)\)” (both integer and floating point)

    Hint

    • To perform lexing and parsing of the new “\(\text{max}(e_1, e_2)\)” and “\(\text{min}(e_1, e_2)\)” operations, you can follow the hints given for \(\text{sqrt}\) above. In addition, you will need to define a token for recognising the comma “,” between the two arguments: you may call this token e.g. COMMA.

    • There are several ways to implement both “\(\text{max}(e_1, e_2)\)” and “\(\text{min}(e_1, e_2)\)” in hyggec. Depending on your approach, you may achieve the result without extending the interpreter, nor the code generation…

    • To implement code generation for “\(\text{max}(e_1, e_2)\)” and “\(\text{min}(e_1, e_2)\)” on integers, the generated RISC-V code will need to perform a conditional jump with a branching instruction, depending e.g. on whether \(e_1\) is smaller than \(e_2\). The implementation for floats is simpler. For an inspiration, see the pattern matching case for Less(lhs, rhs) of doCodegen (in the file src/RISCVCodegen.fs).

Project Idea (Easy): Extend Hygge0 and hyggec with New Relational Operations#

Add some new relational operations to the Hygge0 language and to the hyggec compiler, by following the steps described in Example: Extending Hygge0 and hyggec with a Subtraction Operator — except that you should use the existing expression “\(e_1 < e_2\)” as a reference. Choose at least one operation between:

  • Less than or equal to “\(e_1 \leq e_2\)” (both integer and floating point)

  • Greater than “\(e_1 > e_2\)” (both integer and floating point)

  • Greater than or equal to “\(e_1 \geq e_2\)” (both integer and floating point)

Hint

There are several ways to implement these expressions in hyggec. Depending on your approach, you may implement all of them without extending the interpreter, nor the code generation…

Project Idea (Easy): Extend Hygge0 and hyggec with the Logical Operator “Exclusive Or”#

Add the “exclusive or” operator “\(e_1 \text{ xor } e_2\)” to the Hygge0 language and to the hyggec compiler, by following the steps described in Example: Extending Hygge0 and hyggec with a Subtraction Operator — except that you should use the existing expression “\(e_1 \text{ or } e_2\)” as a reference.

Hint

There are several ways to implement this operator in hyggec. Depending on your approach, you may achieve the result without extending the interpreter, nor the code generation…

Project Idea (Medium Difficulty): “And” and “Or” with Short-Circuit-Semantics#

The Hygge0 formal semantics (Definition 4) omits the reduction rules for the expressions “\(e_1 \text{ and } e_2\)” and “\(e_1 \text{ or } e_2\)” (but you may have written them down as part of Exercise 14, and compared them against their implementation in hyggec in Exercise 20).

hyggec implements the following “eager” semantics for the logical “and” and “or”: they reduce both arguments to values, and then reduce to \(\hygTrue\) or \(\hygFalse\) accordingly.

\[\begin{split} \begin{array}{c} \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-And-L}{$\hygEvalConf{R}{e \text{ and } e_2} \;\to\; \hygEvalConf{R'}{e' \text{ and } e_2}$} \end{prooftree} \;\; \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-And-R}{$\hygEvalConf{R}{v \text{ and } e} \;\to\; \hygEvalConf{R'}{v \text{ and } e'}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{} \UnaryInfCLab{R-And-Res1}{$\hygEvalConf{R}{\hygTrue \text{ and } \hygTrue} \;\to\; \hygEvalConf{R}{\hygTrue}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{$v$ is a boolean value} \UnaryInfCLab{R-And-Res3}{$\hygEvalConf{R}{\hygFalse \text{ and } v} \;\to\; \hygEvalConf{R}{\hygFalse}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{$v$ is a boolean value} \UnaryInfCLab{R-And-Res2}{$\hygEvalConf{R}{v \text{ and } \hygFalse} \;\to\; \hygEvalConf{R}{\hygFalse}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-Or-L}{$\hygEvalConf{R}{e \text{ or } e_2} \;\to\; \hygEvalConf{R'}{e' \text{ or } e_2}$} \end{prooftree} \;\; \begin{prooftree} \AxiomC{$\hygEvalConf{R}{e} \to \hygEvalConf{R'}{e'}$} \UnaryInfCLab{R-Or-R}{$\hygEvalConf{R}{v \text{ or } e} \;\to\; \hygEvalConf{R'}{v \text{ or } e'}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{$v$ is a boolean value} \UnaryInfCLab{R-Or-Res1}{$\hygEvalConf{R}{\hygTrue \text{ or } v} \;\to\; \hygEvalConf{R}{\hygTrue}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{$v$ is a boolean value} \UnaryInfCLab{R-Or-Res2}{$\hygEvalConf{R}{v \text{ or } \hygTrue} \;\to\; \hygEvalConf{R}{\hygTrue}$} \end{prooftree} \\\\ \begin{prooftree} \AxiomC{} \UnaryInfCLab{R-Or-Res3}{$\hygEvalConf{R}{\hygFalse \text{ or } \hygFalse} \;\to\; \hygEvalConf{R}{\hygFalse}$} \end{prooftree} \end{array} \end{split}\]

Example 25

The “eager” semantics of “and” and “or” in hyggec can be observed e.g. by running the following Hygge0 program (available under examples/and-or-evaluation.hyg):

({println("Left of 'and'"); false}) and ({println("Right of 'and'"); true});
({println("Left of 'or'"); true}) or ({println("Right of 'or'"); true})

The output will be:

Left of 'and'
Right of 'and'
Left of 'or'
Right of 'or'

However, many programming languages implement a short-circuit evaluation semantics for both “and” and “or”. The intuition is the following:

  • the expression “\(e_1 \text{ and } e_2\)” reduces to \(\hygFalse\) when \(e_1\) is \(\hygFalse\). The expression \(e_2\) is only considered (and reduced, if needed) when \(e_1\) is \(\hygTrue\);

  • the expression “\(e_1 \text{ or } e_2\)” reduces to \(\hygTrue\) when \(e_1\) is \(\hygTrue\). The expression \(e_2\) is only considered (and reduced, if needed) when \(e_1\) is \(\hygFalse\).

Example 26

With short-circuit semantics for “and” and “or”, the program in Example 25 would only output:

Left of 'and'
Left of 'or'

Write down the reduction semantics rules for “short-circuit and” and “short-circuit or” expressions, and implement them in hyggec. You can choose to either:

  • modify the built-in interpreter and the code generation in hyggec to give new short-circuit semantics to the existing “and” and “or” expressions; or

  • (recommended) add two new operators “&&” and “||” to hyggec. These new operators mean respectively, “short-circuit and” and short-circuit or”, and you should add them to hyggec without altering the existing “and” and “or” expressions (this is similar to the Kotlin programming language).

Hint

  • There are several ways to implement these short-circuit operators in hyggec. Depending on your approach, you may achieve the result without changing the interpreter, nor the code generation. You may even make them simpler by removing some of their existing code…

  • To properly test the short-circuit operator, you need to write some tests that have different observable behaviour depending on whether some part of the short-circuit expression is executed or not. This is not possible with the Hygge0 language — but you can revise the issue in Module 5: Mutability and Loops, when we will introduce Mutable Variables. For example, you may write a test where a short-circuit expression may change the value of a mutable variable (or not), and then write an assertion about that mutable variable…

Project Idea (Medium-Hard Difficulty): Better Output for Assertion Failures#

The goal of this project idea is to improve the usability of assertion failures in the assembly programs generated by hyggec. At the moment, the code generation for assertions (i.e., the case for Assert(...) in the function doCodegen in the file RISCVCodegen.fs) simply generates code that exits the RARS simulator (with an error code) if an assertion fails: as a consequence, it may be hard to understand which assertion failed in the input program.

To improve this, you can extend the hyggec code generation: you can make it generate assembly code that prints some diagnostic information when an assertion fails, before exiting RARS. For instance, you may print an error message with the position of the failed assertion in the input source program.

Note

  • The difficulty of this Project Idea may range from medium to hard, depending on how detailed is the diagnostic output. Please talk with the teacher to agree on an estimate.

  • To report better diagnostic output (e.g., printing the values of the variables involved in a failed assertion) you may revise and improve this Project Idea later in the course — e.g., when we have the tooling to recognise the free variables of an expression.